Behavior cloning / DAGGER

• Requires expert demonstration

• Pro: can be trained offline

• Con: susceptive to “drift”. Fixed with DAGGER

Policy Gradient Methods

Optimizing the policy directly, using various tricks.

REINFORCE

• Takes the derivative through the policy, which amounts to a weighted likelihood optimization

• On-policy model because you need to sample from policy
  • You can make if off-policy through importance sampling

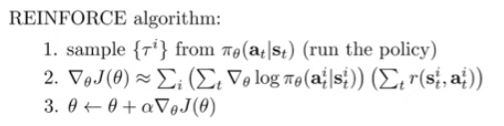
DPG / DDPG

• REINFORCE requires the policy to be stochastic. It turns out that you can do a similar thing with deterministic policies

• As a consequence of being deterministic, it becomes off-policy. See paper for more details

TD3

• builds on top of DPG but uses Q learning techniques to get a better estimation for the rollout weight, including using a double Q function and a slow-updating policy. It uses a SARSA objective, so it is on-policy

TRPO / PPO

• We can show that if we sample from the trajectory distribution under the modified parameter $\theta’$, we can provably improve the RL objective. But this can’t be done; this is like the chicken and egg problem. Therefore, we need to sample from $\theta$ to derive $\theta’$

• We show that we can still provably improve the objective if we keep $\theta$ close enough to $\theta’$.

• TRPO proposes a strict KL bound, while PPO proposes a regularization approach

General method: Actor-Critic

An actor-critic algorithm requires there to be an explicit model for an actor (which does stuff) and a critic (which tells it how good it is). This is a generic framework. The actor can optimize through a policy gradient by replacing the monte carlo rollout with the critic value. Or, it can optimize directly through maximizing the Q function.

The A or the Q function can be fit through Monte Carlo regression or through Bellman Backup.

Depending on which framework it uses, AC algorithms can be online or offline. Often, however, AC methods are on-policy.

Q-Prop

• Use Q functions as a baseline for policy gradient-based AC methods. This reduces variances but requires an additional error term

SAC

Essentially a Q learning method but it is an actor-critic too because there is an explicit representation of the policy. We add entropy, which has a lot of benefits.

General method: Value Methods

These methods focus on learning a value function and then implicitly deriving a policy from it. In reality, Value methods and Actor Critic methods can intersect.

• Policy iteration: improve (implicit) policy using Q or A function

• Policy evaluation: calculating the value of this policy using bellman backup

• Value iteration: combines policy iteration and policy evaluation in one shot.

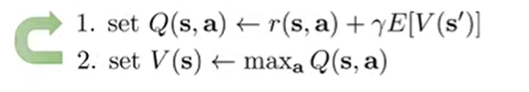
• Fitted value iteration: do the same thing, but with regression objectives. The problem is that we need to sample from the environment.

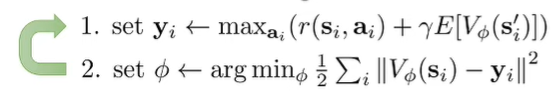
• Fitted Q iteration: we replace V’s with Q’s (see below for another explanation)

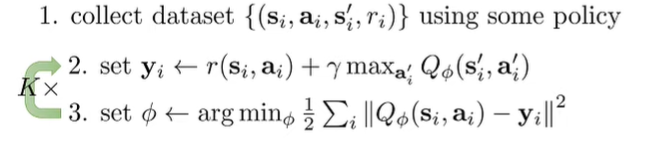
SARSA & Variants

This is a Q function method that uses a bellman backup to compute $Q^\pi$:

This, of course, must be on-policy. We can make the Q function learning off-policy by replacing it with

(this is reminiscient of off-policy actor critic methods. Note that this becomes a SARS method, which is off-policy. You can even ditch the actor and do it implicitly with

(this is the same as fitted Q iteration as seen above). In the actor-critic setup, the last two equations are pretty much the same thing. But in value function methods, the last equation allows you implicitly define a policy.

DQN

This is fitted Q iteration.

Double DQN

• Q functions suffer from optimism bias. To prevent this, just have two Q functions. One we maximize, and one we evaluate.

Double Q Learning (comes later)

• Another approach to solving Q optimism. They use two Q functions and the bellman backup intertwines them, which means that if they are to “cheat” and overestimate, they must agree on this cheat, which is rare.

Offline RL: general methods

Traditional Q learning methods on offline data suffers from over-optimism, because we never get a reality check. A whole set of special tools have been developed for this.

AWAC

• Constrain the current policy to the behavior policy, which gives us a closed-form solution that weighs the likelihood of action under the behavior policy with the learned value.

CQL

• Push down Q values that are OOD as much as possible. We can do this implicitly by sampling from an exponentiated version of the Q function.

IQL

• Optimize the Q function, but the implicit policy is in the support of the behavior policy. They do this using Quantile regression