Why Meta-RL?

Well, we humans learn from reinforcement, but we don’t start from a blank state. We use previous experiences to help us learn very quickly.

Meta-RL: the Formulation

In standard meta-learning, you have a meta-train set that contains different datasets, and then the meta-test set sees how quickly you can generalize to a new task. How does this formulation change for meta-RL?

Well, for Meta-RL, the “tasks” are different MDPs. You assume shared action spaces and state spaces. The only difference between the MDPs is the dynamics and reward function

• inputs: rollouts from an exploration policy in the MDP

• outputs: a policy (or just something that yields further actions)

The big difference is that you are not supplied with the data. You need to create a good learning algorithm as well as an algorithm that collects data in the most meaningful fashion to yield as much information out of the new MDP as possible.

Note how we can have different $\pi^{exp}$ and $\pi^{task}$, where the first one does the data collection and the second one solves the problem. More on this later.

Example: Maze

As a simple example, you might consider a maze environment. During meta-train, you are given various mazes. You need to explore them across various trajectories and solve each maze. During meta-test, you need to solve a new maze.

Black-Box Methods

The black box method looks at making models that we can just plop into a new MDP and adaptation happens as you run the model.

The architecture

The idea here is very simple. You basically make a recurrent model that takes in the state and reward and outputs an action

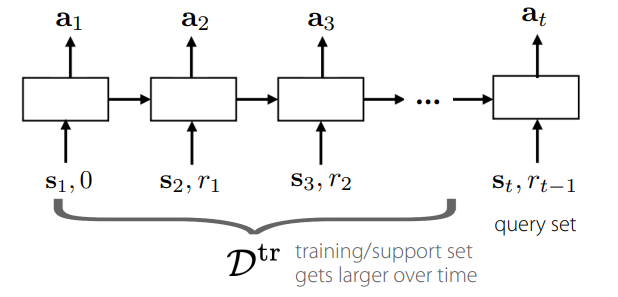
How does this differ from a recurrent policy?

1. A recurrent policy is reset between rollouts. This meta-policy can span multiple rollouts, amassing information in-between

2. This network takes in a reward signal. This allows it to adapt to MDPs where the rewards are different. Remember: the difference in MDPs is the dynamics (inferred through the state) and the rewards.

Now, a recurrent policy is also able to adapt as something changes, but the lack of reward signal input makes the recurrent policy incapable of changing the overall goal. In contrast, this recurrent meta-policy is able to adjust its behavior based on the reward signal and therefore the task.

• Algorithm

  

Training

You train the larger model with an outer RL objective. The objective is just to maximize the expected sum of rewards

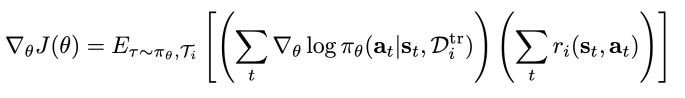
The expected sum of rewards acts as an incentive to explore the world properly, but also to make the appropriate tradeoff between exploration and exploitation.

You can directly optimize the model through a policy gradient, or you can do other smarter approaches. Policy gradient isn’t the most efficient, and this efficiency is on the scale of MDPs, not timesteps (because it’s meta-efficiency). So, we do want a decent amount of efficiency.

You can do off-policy meta-RL by using a recurrent Q function (although this is beyond the scope of our discussion right now). Intuitively, a recurrent Q function takes in the history of interactions (the meta-state) and predicts the final sum of rewards.

Connection to multi-task policies

Meta-learning is basically multi-task learning where the task identifier is derived from the training data in every task. Meta-RL helps adapt to new tasks, i.e. k-shot learning (it does not generalize to completely new goals, which would be 0-shot)

Optimization-Based Approaches

So we know MAML, which is the optimization based approach that yields a “central” parameter $\theta$ that easily adapts to task-specific parameters. How does this map onto the RL problem?

Well, here’s an idea:

1. Using $\pi_\theta$, roll out a few trajectories to form the training data

2. Use classic RL algorithms to adapt $\pi_\theta$ into $\pi_\phi$, using the training data collected by $\pi_\theta$

3. Use the reward from $\pi_\phi$ as the learning signal for the outer loop

Intuitively, this approach automatically creates an exploration policy that is designed to explore the key ambiguities in the environment. Such an exploration policy is also most conducive to fine-tuning, because it naturally contains behaviors that exist in all tasks (otherwise it would be a bad explore). Good exploration and easy adaptability go hand in hand.

Inner and outer objectives

The inner gradient objective is typically the policy gradient. Q learning can’t work very well in the inner gradient because Q learning requires many steps to propagate a signal. However, you can also try using model-based policies.

The outer gradient objective can also be a policy gradient.

As a review: what’s the difference? Well, the inner objective is the traditional RL objective: maximize the expected rewards for this task. The outer objective must account for summed rewards across different MDPs, which means that the outer objective must push for a good exploratory, highly plastic policy. It’s just a difference of scope.

Learning to Explore

The exploration problem is critical in meta-RL, because unlike standard meta-learning problems, we aren’t given the data. We must collect the data in such a way that maximizes our chance at adapting. These exploration strategies may vary on the meta-task.

An indicative test environment

Suppose that the robot has $n$ hallways and the reward is at the end of one hallway. There is a map behind the robot that tells the robot exactly where to go. This is actually a very hard task to meta-learn!

Why? Well, we need a highly functional exploration policy (looking at the map) and a highly functional exploitation policy that uses that information (find the hallway). But we run into a chicken and egg problem

• If you haven’t explored enough, you don’t know how to exploit

• If you haven’t exploited enough, you don’t know what to explore (because exploration is directed by the task)

This chicken and egg problem isn’t just for the hallway problem. This is for any sort of tradeoff between exploration and exploitation.

End to end exploration

You could just try training exploration end-to-end. This is what we were doing in the previous sections on black-box and gradient methods. Essentially, you just optimize for some sum of reward, and you hope that the model will learn to explore and exploit efficiently.

In theory, this works. However, it is a challenging optimization environment. We run into the previously mentioned chicken-and-egg problem. You may not encourage the right explorative behavior if it doesn’t end up in a good state, and therefore, you may not converge to a good exploitation policy either.

The chicken and egg problem arise when we’re trying to make the chicken and the egg at the same time (i.e. learning to explore and exploit). Can we separate these processes?

Thompson Sampling

What if we make the exploration into an explicit process, inspired by bandit algorithms?

You have some latent task variable $z$, a prior $p(z)$, and an inference model $q(z | D_{tr})$ that takes in the exploration data and outputs an estimate of the task. Then, you run the policy $\pi(a | s, z)$. We use a standard Thompson sampling approach that has provable optimality in certain situations.

However, this has some downsides. Your policy will always be trying to exploit, and in reality, there may be a very different exploration behavior that makes the task much easier. In the hallway example, the best exploration is to look at the map, but none of the exploitation behaviors would get you to look at the map.

Intrinsic rewards & Model Prediction

You can also have the model propose its own rewards, which can be helpful for exploration (as the real rewards tend to be exploitative).

You can also optimize for data retrieval and model updates during exploration. However, this may have a weird case where we fixate too much on red herrings (”Noisy TV effect”) because the highest source of randomness will yield the greatest updates / information from the system. Also, if your dynamics are too complicated, you risk running into difficulties.

In general, Thompson, intrinsic rewards, and model prediction are good heuristics, but they can also be pretty bad.

Decoupling exploration and exploitation

The big problem that yielded chicken and egg is the fact that we are learning exploration and exploitation at the same time. We can decouple that!

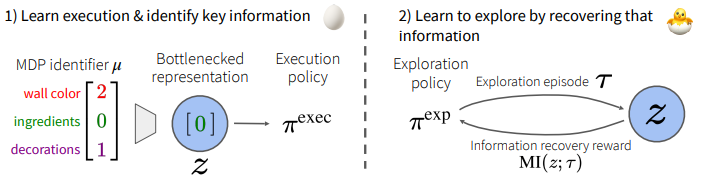
The big idea is to represent the task as some $z$, and this $z$ is passed into the execution policy. We apply an information bottleneck $z$ to make sure that we are encoding in a meaningful way (and ignoring distractors).

To implement this bottleneck, we use the same thing as a VAE: we add noise, and we constrain the magnitude of $z$ (to prevent the model from using magnitude to drown out the noise).

Concretely, this is the algorithm:

Meta-training:

• Train execution policy $\pi^{exec}(a|s, z)$ and encoder $F(z_i | \mu_i)$ to maximize

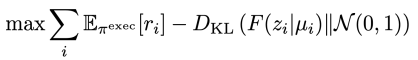
Intuitively, the exploitation policy will try to perform as best as possible, and the encoder will try to push as much information as possible into the $z$ to create the highest reward. To satisfy this constraint, you can just add noise into $z$ and constraint $z$ with an L2 regularizer (instead of doing the whole KL thing).

• Train exploration policy $\pi^{exp}$ such that the collected data $D_{tr}$ is maximally predictive of $z_i$ as supplied by the $F$. There are multiple ways of doing this. One way is to have a prediction model $q(z_i | D_{tr})$ and you train $\pi^{exp}$ through reinforcement learning, using $r_t = L(q(z_i | \tau_{1:t-1})) - L(q(z_i | \tau_{1:t}))$, where $L$ is the prediction loss. The idea is that $r_t$ represents the information gained (through loss lost) of this current step $t$.

Intuitively, the exploration policy will try to get the $q$ to learn as much as possible, and the $q$ will try to use the exploration policy’s data as best as possible. It is a collaborative optimization landscape.

Meta-testing: you explore using the exploration policy, identify the task using the model, and then perform the task with the execution model.

So this sort of formulation is very good. It is efficient and also easy to optimize. The only downside is that it requires a task identifier during meta-training $\mu$.