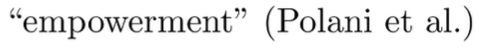• Further reading

  

  

  

  

  

  

Removing the rewards

Human children and other animals interact randomly with the environment without the use of any rewards! There’s some useful body of knowledge that is being learned. Maybe there’s a set of skills we can learn!

The quantities we care about

• $\pi(s)$ is the state marginal distribution of a policy, so $H(\pi(s))$ is the state marginal entropy of a policy. It’s basically how much a policy explores the world.

• The empowerment: $I(s_{t+1};a_t) = H(s_{t+1}) - H(s_{t+1} | a_t)$. This is basically how much control we have over the environment. We want there to be many choices and high amount of control over the next state.

Using imagined goals

Skew Fit Algorithm

One idea of reward-free exploration is to self-propose goals, and therefore self-propose reward structures. This is a bootstrapping approach, where you can become more and more creative with goal generation as your policy gets better.

Concretely, we create a VAE that can generate a goal state $x_g$, and then attempt to reach this goal using a goal-conditioned policy. Use this online data to update the policy and the variational autoencoder.

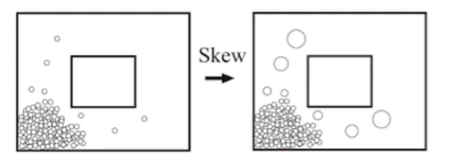
One potential problem is that we need to keep on pushing to create goal states that are slightly out of distribution to encourage exploration. Tod do this, we want to upweight the likelihood of reaching a lesser seen state, or “skew” it. Visually, it looks like this:

We can obtain weights because we can estimate the density score of $p(x)$ through the VAE by computing $p_\theta(x) = \sum_z p_\theta(x | z)p(z)$. This is possible if you have a categorical distribution.

More specifically, you use this weight as we are updating the generative model.

• Algorithm

  

It’s possible to prove that if you use a negative exponent $\alpha$ in the algorithm, the entropy of $p_\theta(x)$ increases, which means that we will converge to a uniform distribution over valid states!

There’s an interesting connection with count-based exploration. Instead of using counts as rewards, we use this measure of novelty to skew the distribution towards these novel states.

What is the Objective?

We’ve derived the skew-fit algorithm, but one common thing to ask is: what is the underlying objective?

• The generator objective is to maximize entropy of goal

• the RL objective is to become better at reaching the goal.

If we get really good, the $p(G|S)$ becomes more deterministic. So, we can write the RL objective as minimizing $H(p(G|S))$. Putting this together, we have the combined objective

Taken together, our objective is

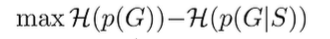
which is just $I(S; G)$. we are maximizing the mutual information between the final states and the goal states! This means that we have high goal coverage and a good ability to hit those goals. It is a very intuitive result.

State-Distribution matching

As we saw in Skew-Fit, our objective was in terms of states and goals. Is it possible to run further with this idea and attempt to fit a policy to a certain state marginal distribution?

An initial implicit attempt

Let’s say that we wanted the policy to have a state marginal that is as high entropy as possible. Can we just create a state marginal estimator and add a reward for being novel WRT this marginal?

Concretely, here’s an initial idea

1. Given $\bar{r} = r(s) - \log p_\pi(s)$, optimize $\pi(a|s)$ to maximize this reward
   1. Note that this is closely related to adding an entropy term in the RL objective, but it’s slightly different. Let’s talk more about this below.

2. Fit $p_\pi(s)$ to fit the new state marginal

There is a subtle problem. Let’s assume that $r(s) = 0$ for a second. In this case, the reward is to minimize the likelihood of $p_\pi(s)$, which basically means changing the policy as much as posslble from the last policy. You end up having a policy progression that chases its own tail.

As you do this, the density estimator will get good state coverage, but the policy you end up with will be arbitrary. It depends on where you stop the policy in the tail-chasing stage. And more importantly, the actual policy doesn’t get the full coverage.

Explicit Matching: Attempt 1

Instead of implicitly adding a reward augmentation (which didn’t really work), can we be more explicit on matching state marginals? For example, can we optimize this?

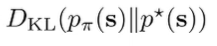
We can write the reward as

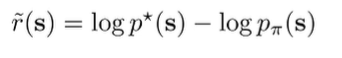
and the RL objective under this reward is exactly the KL divergence.

However, RL doesn’t exactly do this! RL isn’t aware that $p_\pi$ depends on $\pi$ (because there are no gradients), which means that we still get suboptimal tail-chasing problems. In fact, this is no different than our previous non-example, with the difference being a constant value $p^*(s)$.

Resolving tail-chasing behavior (Attempt 2)

The original algorithm was like this

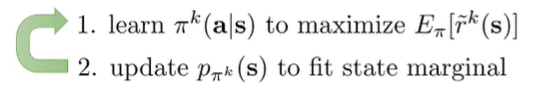
which had the tail chasing behavior. But we have a pretty simple resolution. What if we fit a state marginal to estimate all the state seen so far, instead of the current state marginal.

We also return $\pi^*(a|s) = \sum_k^{\pi^k}(a|s)$.

• Algorithm

  

This works because $p_\pi(s) = p^*(s)$ is the Nash equilibrium of a two-player game. It’s a game between the exploration policy and the density. It makes sense because the exploration policy is essentialy carving out a path, but this path becomes immediately something to avoid. Once the states are matched, there is nowhere more to carve out, but the cost is that now everything needs to be avoided.

And because we know that this is a Nash equlibrarium, we know that we need to return the mixture (from game theory results).

When is state entropy helpful?

In Skew Fit: we compute $\max I(S; G)$ and in SMM in the the special case where the marginal is uniform, we are computing $\max H(p_\pi(S))$.

When is this a good idea? If you want to adversarially give the worst possible goal and the robot knows, then the best distribution is uniform. This is a result that shows from maximum entropy modeling.

Do you see why we can’t practice for the worst case situation, because the adversary will know? It’s better to be versatile.

Learning Diverse Skills

Previously we talked about state distribution objectives, but can we be more abstract. Can we have maximum entropy skill objectives?

Let’s say that we have a policy $\pi(a | s, z)$ where $z$ is a task index. Can we self-supervise train a policy that performs maximally different skills per $z$?

You can use a diversity-promoting reward function, which means that we should reward states that are unlikely to occur for other task

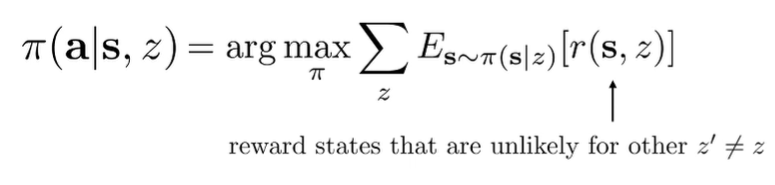
You can just have the reward be a classifier

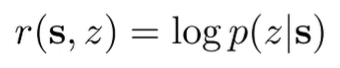
Note that this is not an adversarial paradigm. You’re actually trying to make the classifier’s job easier!

We can also understand the above objective as maximizing $I(Z, S)$. This is because $H(z)$ is maximized if you have a uniform prior $P(z)$, and $H(Z | S)$ is maximized by maximizing the reward objective $\log p(z | s)$