Stochastic programming

This dives deeper into some fitting applications. In this particular case, we have functions $f_i(x, \omega)$ that depend on $x$ and some random variable $\omega$. We know the distribution of $\omega$. How do we pick $x$ with constraints that are satisfied on 1) average or 2) with high probability, and with objective that is small on 1) average or 2) with high probability.

The formulation

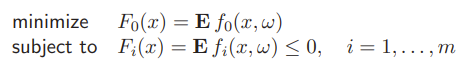
the $f_i$ is convex in $x$ for each value of $\omega$, so the stochastic programming problem is convex. Sometimes there’s an analytical formulation of this expectation, other times we must approximate. More on this approximation later.

Certainty equivalent approximation

We can replace the outer expectation with an inner expectation

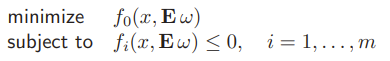
Essentially, we ignore the parameter variation. Because $f$ is convex, Jensen’s inequality states that

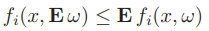
which means that this solution is a lower bound on the optimal value.

Expected violation, shortfall constraints

We can change the types of constraints to match the problem we want to solve. For example, we can instead search for the expected worst violation (which is also convex)

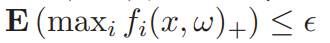
or instead, we might add a soft penalty by adding the constraint to the objective

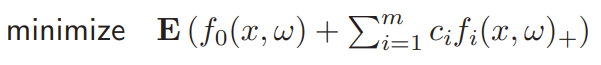
Chance constraints, percentile optimization

This is constraining the chance that something happens

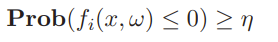
this is convex in some cases. You can also try to optimize the percentile that something happens

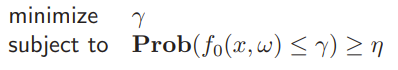
This is convex or quasi-convex in some cases.

Approximating stochasticity

Finite event set

If the events are finite, then you can simply express the whole expectation in a tidy sum

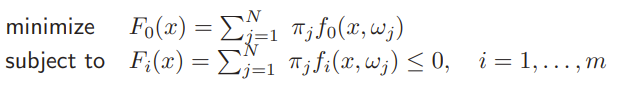
Monte Carlo

Just generate $N$ samples $\omega_1, …, \omega_n$ and assign uniform probabilities to each one. Then, make average approximations

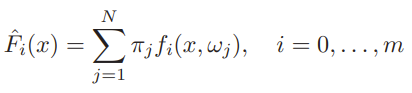
We can validate using a second set of samples in the validation set.