Optimization

Optimization is trying to minimize an objective function while following certain rules (inequality and equality constraint functions)

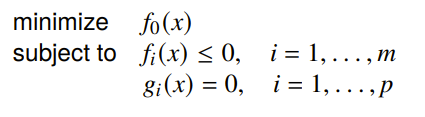
Types of optimization

• Least squares: no constraints and the objective is of the form $||Ax - b||_2^2$.
  • Analytical solution with $O(n^2k)$ complexity

• Linear program: if objective and constraint functions are linear $f_i(ax + by) = a f(x) + bf(y)$
  • No simple analytical solution, but some very effective methods like Dantzig’s simplex method

• Convex optimization $f_i(ax + by) \leq a f(x) + b f(y)$ (this is just the convexity definition; more on this later).
  • We don’t care about how much we use the constraint, as long as we don’t violate it

• Nonlinear program
  • Hard to solve, requires assumptions and relaxations. Local optimization is popular, like gradient descent.

Uses for optimization

• a lot of real-world requirements like fuel optimization, landing controls,. etc

• Worst-case analysis (see if your system can handle something really bad, but you’ll need to find this worst-case first).

• Model certain real-world phenomenon, which surprisingly follows objective optimums quite closely

Convex Optimization

Convex Optimization is a special form of the general optimization problem, where all equality constraints are linear and all inequality and main objective functions are convex, i.e. upward curvature. Now, this might sound easy, but we didn’t talk about how many contraints and variables. We might be dealing with thousands of variables and many, many contraints.

The cool part about convex optimization is that as soon as you can get a problem into convex form, you can pull the crank and get a solution. There is no art in finding this solution.

Solving convex optimization problems

There are many different convex optimization approaches that we’ll talk about. Interior point and first order methods are common, and these work out of the box without needing initial guesses or tuning. These are also quite lightweight and easy to implement.

Generally, there is no analytical solution, but there exists some efficient iterative algorithms.