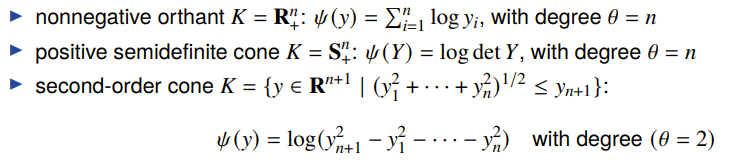Inequality Constrained Minimization

We have the following setup

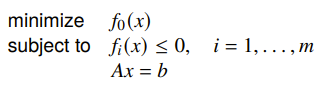
where $f_i$ is convex. How do we solve this sort of problem?

Assumptions

We assume that the problem is strictly feasible, which means that Slater’s constraint holds, meaning that there exists some $\lambda^*, \nu^*, x^*$ that satisfy the KKT conditions

Log-barrier and Central Path

We might start by thinking that we could turn the inequality constraint into the objective by adding an infinity-indicator function

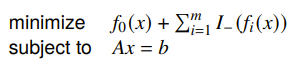
Now, this would technically run, but it would be terrible. The method would just break every time it hits the barrier. But what if we make it smooth?

Log-barrier

This is where the log-barrier comes in, which is a function that we’ve seen before.

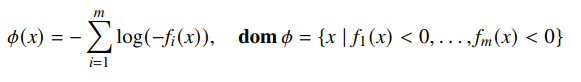
This function is effectively approximating the indicator function but in a smooth way.

This function is convex from composition, and it is also twice continuously differentiable, which is good because we want to apply something like Newton’s method

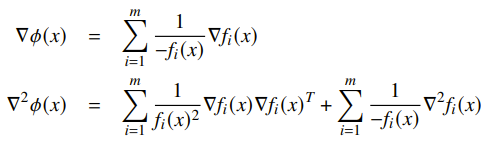
The approximation

We can approximate the indicator function using the log-barrier. It is no longer the same problem, but it has the same properties.

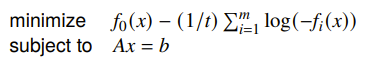
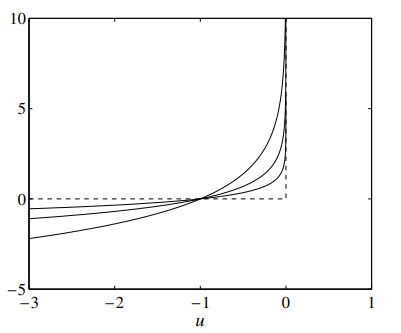
Or, namely: the larger the $t$ the closer we are to the original problem, but the sharper the bend. It’s a tradeoff.

Central path

Let $x^*(t)$ be the solution of

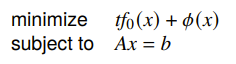
If $x^*(t)$ exists and is unique, then the central path is the set

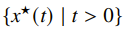
Intuitively, as $t$ grows larger, we get closer to the true optimal by edging closer and closer to the edge of the feasible space. Here’s an LP as an example:

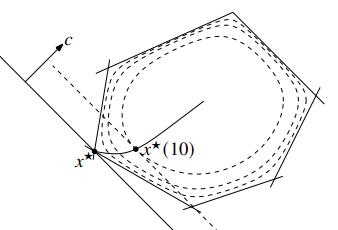
Note that here, the path does change with irrelevant constraints because these constraints still change the different forces at play.

Duality Interpretation

There’s an interesting connection to duality. Recall that we set up the dual problem by essentially adding a “soft” penalty through the $\lambda, \nu$. Now, let’s talk about duality of this log-barrier problem.

Establishing a lower bound on optimality

Because of strong duality for every $t$, we can just use the KKT conditions to assert that $x$ is optimal if there exists some $w$ such that

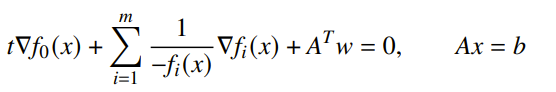
Every central point has a dual feasible point too. Let’s define

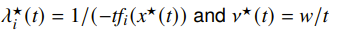
We assert that this choice is a dual feasible point. To prove this, we plug this choice into the Lagrangian

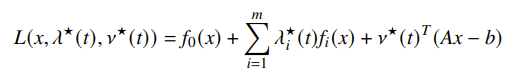
If we simplify and attempt to maximize, we’ll actually get the exact equation for $x$ that we got from strong duality. This tells us that $x^*(t)$ minimizes the Lagrangian. This in turn tells us that

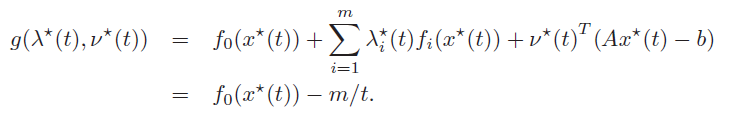
which immediately gives us a very nice bound on the optimal value:

Interpretation through KKT

If we let $x = x^*(t), \lambda = \lambda^*(t), \nu = \nu^*(t)$, then we satisfy KKT conditions, except that we have “approximate” complementary slackness

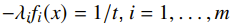
that becomes true slackness when $t →\infty$. This interpretation comes from just rearranging our definitions of $\lambda^*$.

Force field interpretation

You can imagine $t f_0(x)$ as the potential of the force field that pushes us to optimize the real objective, and $-\log(-f_i(x))$ is the force field that pushes you to avoid the boundary. The forces balance at one point, and this balancing shifts with $t$.

Barrier Method

The barrier method takes the insights we made in the previous section and just turns it into an algorithm. You iteratively compute $x^*(t)$ by minimizing $tf_0 + \phi$ with $Ax = b$, and then you just keep on doing this until you get close enough.

The stopping criterion is inspired by the duality gap. The centering step might be complicated, so we turn to Phase 1 methods that can get this job done.

Phase 1 Methods

The Barrier method requires a strictly feasible starting point, but what happens if that’s hard to find? Here, we consider the phase 1 methods, which forms an optimization problem that is strictly feasible and finds a strictly feasible point for the original problem. If none exists, then it tells you where the problems are.

Slack variable formulation

The idea is this: introduce a slack variable for each constraint and minimize

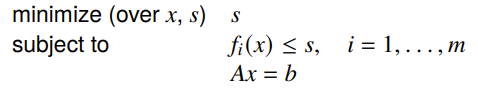
You can pick $s$ such that your initial choice of $x$ makes this problem feasible. Then, after running everything, as long as all $s$ is less than zero, you’ve got a feasible original problem. You can take the $x$ you obtained from the problem and use it to initialize the barrier method.

To prove infeasibility, we can use the dual variable. If we find some dual feasible point with a positive dual objective, then we know that $p^* > 0$ and therefore it must be impossible.

Sum of infeasibilities methods

Instead of finding a single slack variable, you minimize the sum of a slack variable set. This is useful because it can tell you which inequalities are impossible to satisfy.

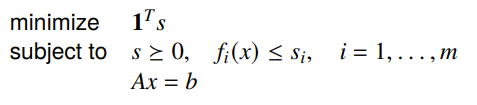
We can also weigh the different slack variables by the priorities in satisfying the constraints. Generally, this approach can find better solutions.

Complexity of barrier method

There’s a lot of not-so-fun math, but the final result is that the number of iterations is

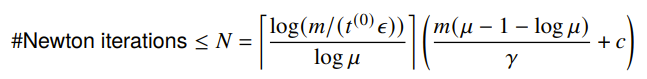
As $\mu$ increases, the iterations decreases. If we set $\mu = 1 + 1/\sqrt{m}$, we have

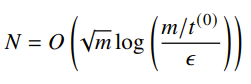
which means that the barrier method is polynomial in $m$, the number of variables.

Generalized inequalities

What if we want to satisfy some other type of inequality, i.e. what if the functions are not scalar valued?

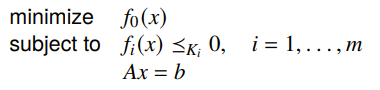
General logarithm

We define $\psi: R^q → R$ as the generalized logarithm for a proper cone $K$ if…

• The domain is the interior of $K$

• The hessian of $\psi$ is strictly negative definite

• we have $\psi(sy) = \psi(y) + \theta \log s$ where $\theta$ is the degree of $\psi$.

There are many formulations of this (unlike the single formulation of the log barrier), including these examples:

• Examples

  

Log barrier and central path

You just replace the logarithm with the general logarithm in the barrier function