Tips

• determinant of some scaling matrix often corresponds to the area

Extremal Volume Ellipsoids

This is a general class of problems where we want to find an ellipsoid that satisfies some constraint but minimally.

Minimum around a set

The Lowner-John elipsoid is the minimum volume ellipsoid such that a set $C$ is fully contained within it. We approach this problem by parmeterizing the ellipsoid as

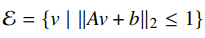
And the volume of the ellipsoid is proportional to $\det A^{-1}$, so the objective is just

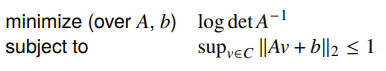
This is convex but the constraint can be hard to evaluate if $C$ is general. The finite set, of course, is straightforward.

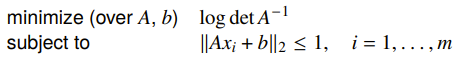
It gives us the ellipsoid for the convex hull of $x_1, …, x_m$.

Maximum inscribed ellipsoid

If we have a convex set, what is the maximum volume ellipsoid that can be inside a set? This time, we need to parameterize $\epsilon$ as the following:

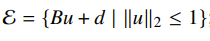
i.e. the transformation of a unit ball. The objective therefore becomes

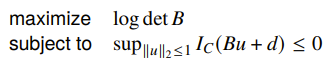
This is hard for general $C$, but if $C$ were a polyhedron, then the objective becomes

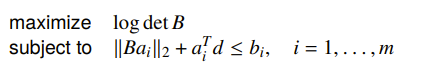
Relationship between covering and inscribing

The Lowner-John ellipsoid when shrunk by factor $n$ lies inside $C$ (where $n$ is the dimension). The maximum volume inscribed ellipsoid, when expanded by $n$, covers $C$. So you can actually derive coverage and inscribing from each other.

However, it’s worth noting that the minimum inscribed ellipsoid takes a polyhedron, while the Lowner-John ellipsoid takes in a set of points. The minimum inscribed ellipsoid is NP-hard if it takes a set of points (it’s not easy to make a polyhedron from a set of points).

Centering

The centering problem is to find something that is in the middle of a set. The Chebyshev center is the center of the largest inscribed ball, and we showed that we can find this through linear programming. We can also find the center of the maximum volume inscribed ellipsoid and other centers, which we will get into here!

Analytic center

The analytic center of convex inequalities and the constraint $Fx = g$ is the solution of

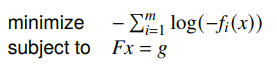
Note that this is the log-barrier function. If you want $f(x) \leq 0$, the function physically prevents you from violating. Because these functions are involved increating the log-barrier, functions that describe the same set can yield different ananlytic centers.

Graphically, the analytic center can be visualized as sort of a “smoothing” out of the edges. We can see the level curves of this function as follows

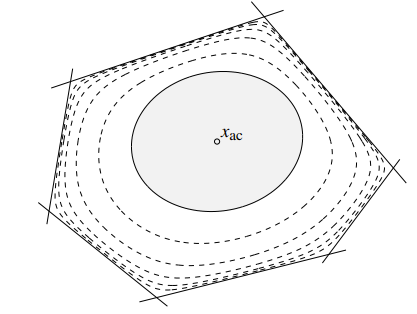
You can create inner and outer ellipsoids from the analytical center:

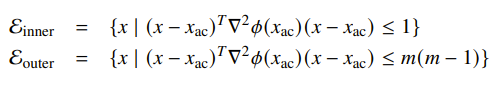
Essentially, you use the shape of the ellipsoid defined at the analytic center, and then you expand it outwards.

Classification

The idea of classification is pretty straightforward. We can start with formulating a feasibility problem: find a $a$ such that

This is just an LP feasibility problem and it is convex. This function is homogeneous in $a, b$ , so the more common formulation is

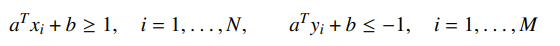
We could make things a bit more interesting by adding a maximum margin objective, which is essentially maximizing the distance you can put between the two sets

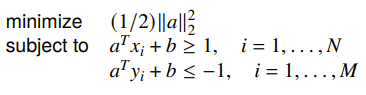
This is because the Euclidian distance between hyperplanes i

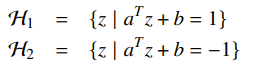
is $2/||a||_2$.

Approximating linear separation

The way you do this is to introduce slack variables as follows:

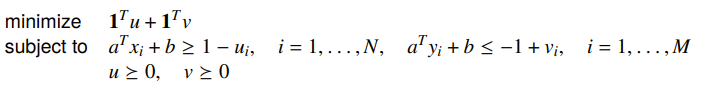
The support vector classifier just brings this approximation and adds the maximum margin objective on top

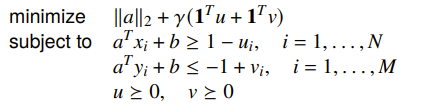
Nonlinear discrimination

You can use a kernel function set $(F_1, …, F_k)$, and your objective is still linear:

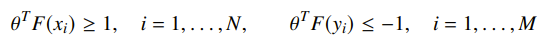
As long as you don’t actively tune the kernel function itself, adding a kernel does not change the complexity of the problem. Commonly, you use a quadratic or polynomial component.

Placement, Facility Location

Say that you had $N$ points in $R^2, R^3$. Some positiosn are given and some are varibles. For each pair of points, you have a cost function. The goal is to minimize the pairwise sum of cost functions.

Common interpretations is the points as being warehouses and the cost function is the transportation cost. You can think of a lot of other analogies similar to this.

As long as the cost function is convex, this is definitely a convex problem.