Equality-Constrained Minimization

This is when you want to solve the problem

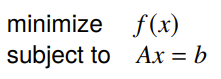
where $A \in R^{p\times d}$ where the rank is $p$, i.e. there’s probably fewer constraints than variables, meaning that there will be a non-zero space of potential solutions that satisfy $Ax = b$.

From the discussion of KKT conditions, we established that we can solve this constrained problem by solving this alternative problem

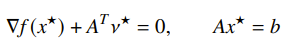
Of course, this is impossible to solve directly. But we can start at the quadratic and go from there.

Quadratic Minimization

If our function is quadratic,

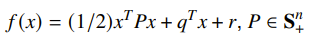
then the KKT condition can be expressed in the KKT Matrix

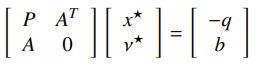
IF the matrix is nonsingular, there is a unique primal-dual pair. If the matrix is singular, then any solution is an optimal pair. If the system is not solvable, the problem is either unboudned or infeasible.

The matrix is nonsingular if and only if $Ax = 0, x \neq 0 \rightarrow x^TPx > 0$ (PSD on nullspace of $A$.)

Eliminating equality constraints

You can remove the equality constraints by expressing the set $\{x | Ax = b\}$ as $\{Fz + \hat{x}\}$ where the range of $F$ is the nullspace of $A$ and $\hat{x}$ is some solution of $Ax = b$. This gives you the unconstrained problem of minimizing $f(Fz + \hat{x})$.

Once you have the solution $z^*$, you can solve for

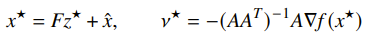
Solving through the dual

You could potentially solve the dual of the objective and then recover the primal by minimizing (because it satisfies strong duality). The dual is

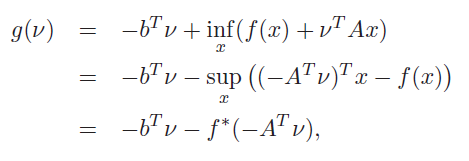
and this gives you an unconstrained problem.

Newton’s method with equality constraints

You can approximate any function as a quadratic with the hessian, which gets us the following KKT matrix

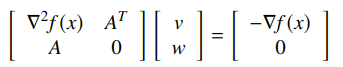
This newton step solves for the $\nu$ that minimizes the local quadratic, and you can take a step in this direction (or dampen it).

Newton decrement

We define the Newton Decrement for the equality constraint as

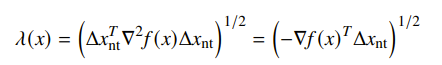
Note that this is slightly different from the definition in the unconstrained case. However, the function is still the same: estimates $f(x) - p^*$, and directional derivative in the newton direction.

The algorithm

Infeasible start Newton method

Newton’s method described previously only works when we start at a feasible point. But what happens if we don’t?

The intuition is that we want to step towards being feasible and optimal.

Newton step at infeasible points

We have this objective from before

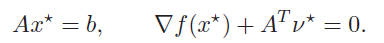
If we have some current $x$ (which may not be feasible), we want to take some step $\Delta x$ such that $x + \Delta x = x^*$. How do we do this? Well, let’s substitute in $x + \Delta x$ into the constraint and use the first-order approximation

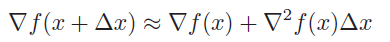
which gets the revised objective

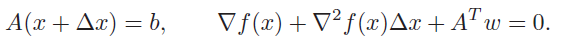
Note how this is different from traditional Newton step, where we could just solve the linear equation. We had to take a slightly different route because of the infeasibility. Finally, this gives us the revised equation

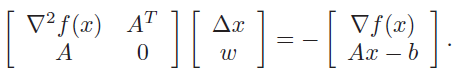
Note that the $w$ isn’t the dual parameter; we’ll get to the dual interpretation in the next section

Interpretation as primal-dual step

Let’s define the primal-dual residual as

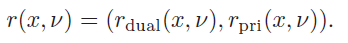
and we want to get things to zero. To do this, we make the tuple $y$ and set out to make some $\Delta y$ such that

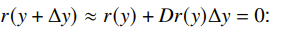
If you write it out, you’ll get the equation

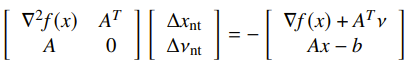
The algorithm

In practice, we use the primal-dual setup to solve for the primal and the dual variables.

Implementation

Solving KKT systems

Both types of constrained Newton methods require you to solve matrices like this

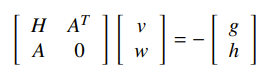
The LDL factorization is helpful here