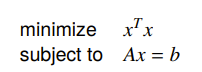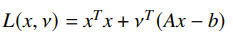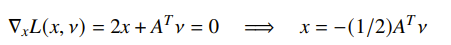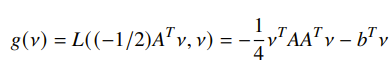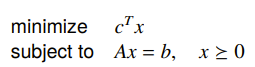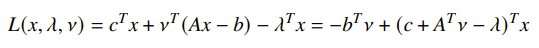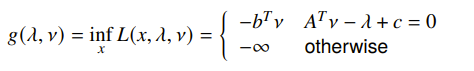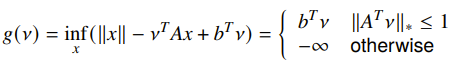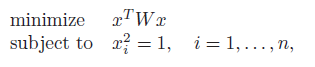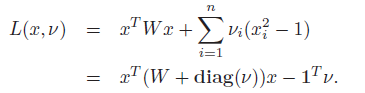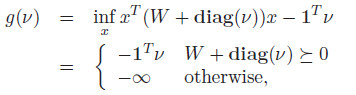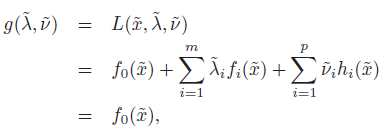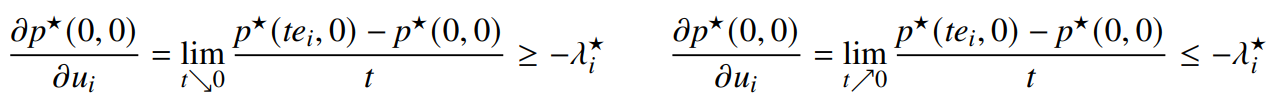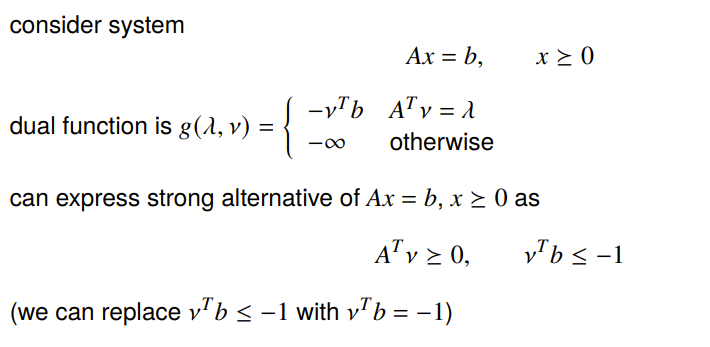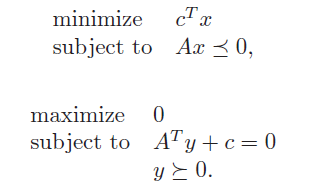Lagrangian

The standard form optimization problem has this format:

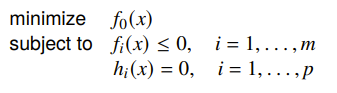
We can construct the Lagrangian as the following equation:

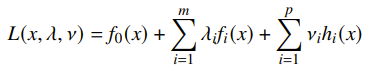
where $\lambda_i, v_i$ are lagrange multipliers. Intuitively, you can understand the Lagrangian as treating the constraints as a form of cost and revenue. if you don’t reach the constraint, it can help you reach a lower objective. If you exceed the constraint, you incurr a cost. We’ll talk about how we can extend this to hard constraints later.

• Matrix and vectors

  If you have a vector inequality, you can usually express this as an inner product with some vector $\lambda$. For example, if you have $v \prec 0$, then it becomes $\lambda^T v$ (think about this for a second).

  If you have a matrix inequality, it naturally makes sense that you would compute the matrix inner product, which is just $tr(Z^TX)$, where $Z$ is the Lagrange matrix.

Lagrange dual function

So in the Lagrangian, we introduced the multipliers. This feels weird, and we’re not quite sure about what they do. So we formulate the Lagrange dual function, which looks at how the multipliers behave as the function of the minimization across $x$.

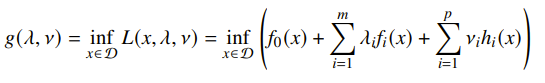
Turns out that this $g$ is concave. $L$ is an affine function of $\lambda, \nu$ for each $x$. The infimum of a bunch of affine functions, which is concave. You might find that some values of $\lambda, \nu$ create unbounded optimziation problems. This has significance that we’ll talk about later.

Dual function is a lower bound ⭐

$g(\lambda, \nu)$ is also a lower-bound on the optimal value of the problem. This is easily proven through the definition. As long as you have a feasible $\tilde{x}$, then the following is true, by properties of $f$ and infimums.

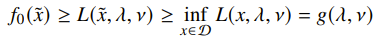
If you can find a closed-form expression for this $g$, then you can have a good lower bound on the true constrained optimization.

• Example: least-norm to linear equations

  If we have

  

  The Lagrangian is

  

  Then you can have a closed form expression for solving the lagrangian

  

  and this gets you a general expression for $g(v)$:

  

• Example: standard LP

  If you have

  

  Then the lagrangian is

  

  And because this is affine, we notice that the infimum has a pretty interesting property:

  

• Example: equality constrained norm minimization

  If we have

  

  then the dual function also has a special domain

  

  where $||v||_* = \sup_{||u||\leq 1}u^Tv$, otherwise known as the dual norm.

• Example: two-way partitioning problem

  If we have

  

  this is equivalent to cutting the vector into 1 and -1, such that some objective is optimized. Turns out, you can have Lagrangian as

  

  And so the dual is

  

Relationship to Conjugate function

It turns out that there is a pretty neat connection between the Lagrange dual and the conjugate function. Lets say that we had this set of constraints in an optimization problem:

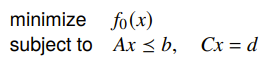
If we write out the dual function, we’ll see

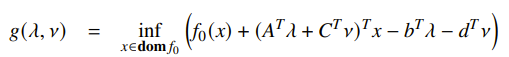
And if we remember the definition of the conjugate function as $f^*(y) = \sup_x(y^Tx - f(x))$, you can rewrite the dual as

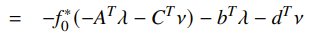
This is useful because if you know the conjugate of $f_0$, the dual is trivial to compute.

Linear approximation interpretation (the taxation interpretation)

While this has cool mathematical properties, it also has some important intuitive properties. In the hardest case, we have

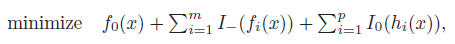
where the indicator function is $\infty$ when the constraint is violated. This represetns a sort of “infinite displeasure” at violation. The Lagrangian is the same formulation except that the indicator functions are replaced with linear approximators which represent as “soft” displeasure.

So this is a really nice diagram. The solid line is the objective, the dotted line is the constraint. The valid points are between the vertical lines. The “haze” around the solid line is the Lagrangian function with different values of $\lambda$. See how they form a lower bound for everything inside the feasible set?

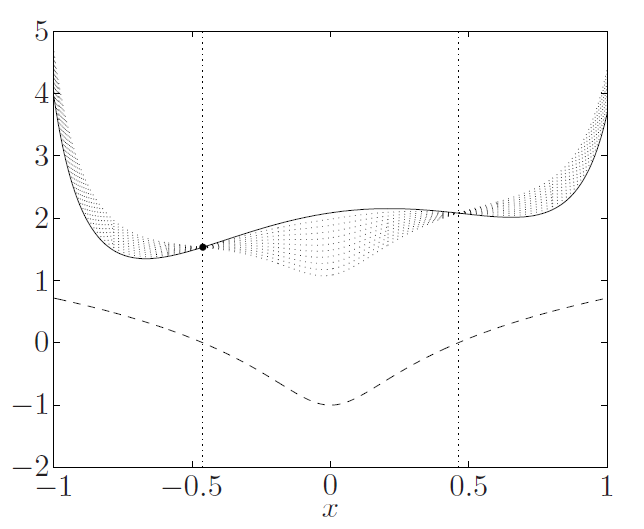
Lagrange Dual Problem

We previously established that the Lagrange Dual provides a lower bound on the optimal value $p^*$. But what is the best lower bound? In other words, can we get really close to the optimal value? For this, we present the dual problem:

Because $g$ is concave, this is a convex optimization problem, even if the original problem (known as the primal problem is not). We denote the dual optimal value as $d^*$.

We’ll notice an interesting property: there are certain constraints in the primal problem that turn into implicit constraints in the dual problem (i.e. if you don’t follow such constraints, the dual problem will yield negative infinity.

Adding implicit constraints

Make sure to look at the infimum carefully, especially if you’re dealing with an LP. Often, with an LP, you’ll get somethign like $(K + B + N)x - \lambda…$. In this case, the infimum goes to negativity infinity unless $K + B + N = 0$. Make sure that you add these implicit constraints into your dual function before your blindly take the gradient.

Types of Duality

Weak Duality

The weak duality is just a restatement of our old derivation: $d^* \leq p^*$. This holds true for any sort of problem (because the dual is a lower bound), and we can use this to find non-trivial lower bounds of potentially difficult problems.

Strong Duality ⭐

The other form, strong duality, is much more interesting. This is when $d^* = p^*$, and it doesn’t hold in general. In general, if you see an LP, you can assume strong duality because of Slater’s constraint. You can also use this as a certificate of optimality. If you have $f(x) = g(\lambda)$, then both parameters are optimal (because we know that $g$ is a lower bound of $f$).

Slater’s Constraint

If the problem is strictly feasible, i.e. there exists some $x$ such that

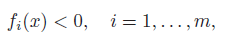
then strong duality holds. If $f$ is affine, we can exclude it from Slater’s constraint. Vacuously, if all $f$ is affine, then strong duality automatically holds. IF there are no inequalities, then feasibility is all we need.

Primal and dual relationships

Note that when we started, we had the Lagrangian function

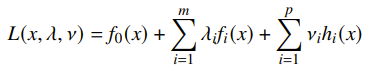
Let’s think about the primal problem. At each feasible $x$, we can say that $f(x) = \sup_{\lambda \geq 0, \nu} L(x, \lambda, \nu)$. This is because if $f_i > 0$, then the supremum would push everything to infinity. Likewise, if $h \neq 0$, the supremum could push everything to infinity. As such, the optimal value of the primal problem is

Let’s marinate on this for a second. The primal problem will either be infeasible, or the inner supremum yield $\lambda, \nu$’s that are zero.

Let’s contrast this with the dual problem, which has

Let’s think about this. In some cases, the $\inf$ yields $-\infty$ and therefore makes the outer problem infeasible. This is similar to the primal version of the problem.

We know from our previous discussions that $d^*$ is a lower bound for $p^*$. But what happens with strong duality? Well, we’re essentially saying that

This actually has two very neat interpretations. First, if we think about this setup as a min-max game, this tell us that either player gains an advantage by going first. This is generally not true without strong duality.

Second, this tells us that $(x^*, \lambda^*)$ form a saddle point of the Lagrangian if there is strong duality. In other words,

conversely, if $(x, \lambda)$ is a saddle point of the Lagrangian, then $x$ is primal optimal and $\lambda$ is dual optimal.

Geometric Interpretation of Duality

Initial interpretation

Let’s try to understand the meaning of the dual function geometrically. Let’s start with one constraint $f_1(x)\leq 0$ and an objective function $f_0(x)$. We can plot the values on the x-y axes with a section $G$ for the achievable values of $f_0, f_1$ as $t = f_0, u = f_1$

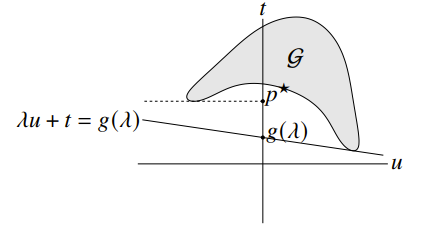
We define the dual function as $g(\lambda) = \inf_{u, t}(t + \lambda u)$. Note that we do inf u, t which is implicitly $\inf_x f_0(x) + \lambda f_1(x))$.

Let’s start with the function $t + \lambda u$. This is a set of non-vertical lines of slope $-\lambda$. It is minimized when it touches $G$ because the level curves are all pointing in one direction (and it’s positive). So the line has $g(\lambda)$ value all throughout, so the t-intercept has $t = g(\lambda)$.

You can start to understand why the lower bound condition is true, and perhaps you can start to visualize which conditions of $G$ are required to have strong duality.

Epigraph variation

If we consider the epigraph $f_0(x)\leq t$ as part of the valid set (think about this carefully), this gets you a new set $A$. Previously, $t$ was a free-floating value that we wanted to minimize. Now, because it’s drawn as the feasible region, we know that the optimal value will occur at the edge of the set $A$, and more specifically, as $A$ crosses $t$ axis.

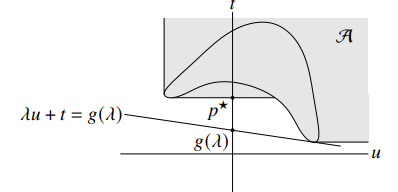
This allows us to formulate the strong duality restriction quite cleanly: if there is a non-vertical supporting hyperplane at $(0, p^*)$, then it is strong duality. This is true for convex problems because $A$ is the convex epigraph.

Without getting into too much details, Slater’s condition guarantees that here exists some $(u, t)\in A$ with $u < 0$, which prevents a vertical supporting hyperplane from forming.

KKT Conditions

The KKT conditions are some properties that tell us neat things about optimality. For convex solutions, satisfying KKT can mean that we satisfy optimality, so it gives us another objective.

Complementary Slackness

To contextualize the KKT condition, we start with dual optimal definition

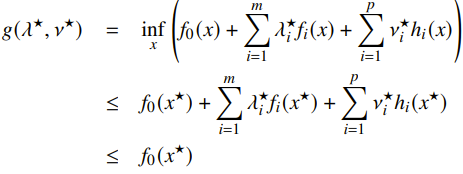
Now, if strong duality is satisfied, then we know that the two inequalities are equalities. There are some interesting upshots we can take from this observation. First, because the second inequality is an equality, we conclude that $x^*$ minimizes $L(x, \lambda^*, \nu^*)$ (it may not be the only value that minimizes).

We also conclude that

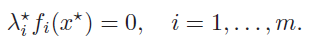
Which brings us to the idea of complementary slackness: at the optimal point, the function is either zero (tight) or we assign no dual weight $\lambda$ to it.

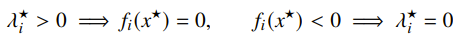
Intuitively, this says that if strong duality is upheld, then the optimal value Lagrangian assigns non-zero $\lambda$ to constraints that are active.

The KKT Conditions

If we have strong duality, let’s consider the relationship between $x^*$ and $\lambda^*, \nu^*$. The lack of duality gap states that $x^*$ minimizes $L(x, \lambda^*, \nu^*)$ over $x$. Therefore, the gradient of $L$ at that point must be zero.

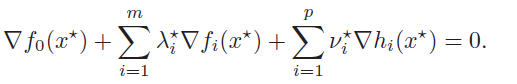
Therefore, we have the following conditions, which are known as the KKT conditions

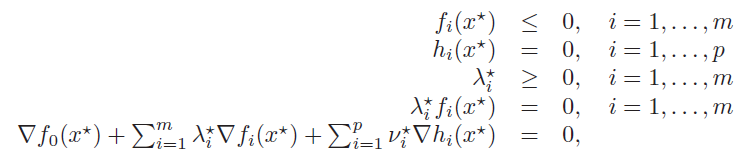
Any $(x^*, \lambda^*, \nu^*)$ must satisfy these conditions for a strong duality setup.

Using KKT Conditions on convex problems

Normally, the KKT conditions are necessary but not sufficient for optimality. But if the primal problem is convex (and strong duality), the KKT conditions are also sufficient.

• Proof

  

  The third equality is complementary slackness. The first equality comes from the gradient vanishing and convexity.

  Because $g(\lambda, \nu) = f_0(x)$ and ordinarily it’s a lower bound, we know that we’ve reached optimality.

In some cases, it is possible to solve KKT conditions exactly. Many algorithms for solving convex optimization (like constrained Newton’s methods) are just solving KKT.

For example, if you want to minimize a linear-constrained quadratic

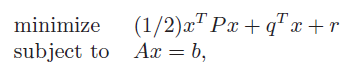
The KKT conditions are

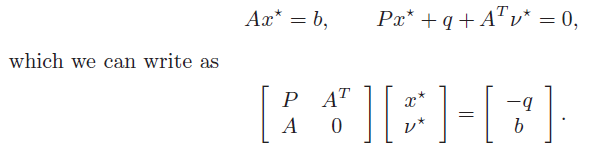
If we solve this linear equation, we get the optimal primal and dual variables.

Solving primal with dual

From above, we know that with strong dual problems, $x^*$ minimizes $L(x, \lambda^*, \nu^*)$. So, if you had the optimal $\lambda^*, \nu^*$, you can solve for the primal by just doing

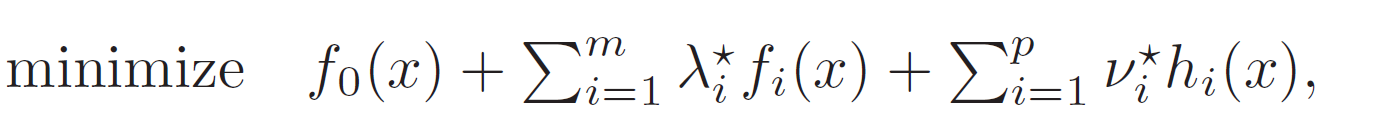
Note that we are not guarenteeing that $f$ is a convex function, so we might have multiple solutions, or no solutions at all. If the solution is not primal feasible, then no primal optimal point can exist.

This structure is helpful if the dual problem is easier to solve than the primal problem.

Sensitivity Analysis

In sensitivity analysis, we are interested in how the solution changes as we change some of the boundaries of the constraints. We start with the unperturbed problem

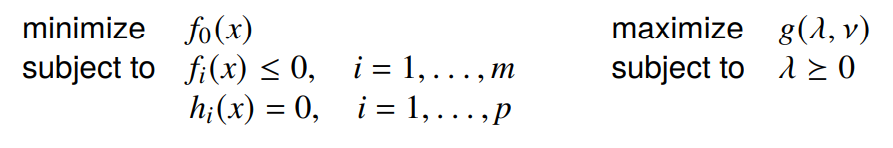
And we can get the perturbed problem and the dual

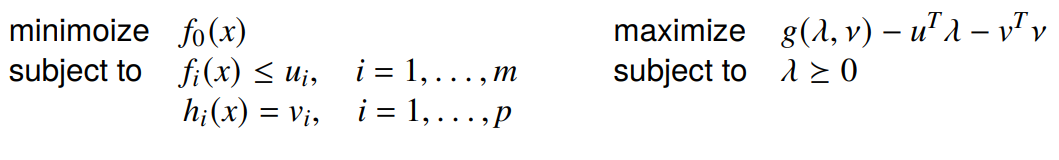
We can formulate the optimal value as a function of $u, v$: $p^*(u, v)$.

Global sensitivity via duality

If strong duality holds for the unperturbed problem, we can apply weak duality and substitute in the strong duality assumption

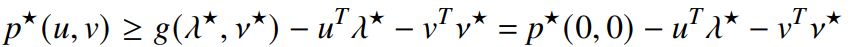
So this tell us a lot of interesting things (mostly, we can tell when things get worse becuase it’s a lower bound)

• If we tighten constraint by making $u < 0$, the rate that $p^*$ increases depends on $\lambda^*$.

• If $v^*$ is positive, then taking $v > 0$ will increase $p^*$

• IF you stare at this for awhile, you’ll see other sensitivities

• List

  

These results remind us about a deeper truth of what the multipliers mean. They are telling us how much we care about a specific constraint, as in, if we made the constraint tighter, how much we would lose.

Local sensitivity via duality

You can take a deeper look at $p^*(u, v)$ by taking the derivative. We know that

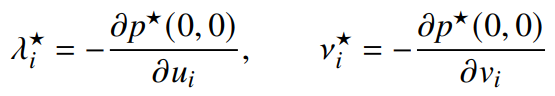
from the global sensitivity result. Unlike the global sensitivity result, local sensitivity is not asymmetric; it tells you exactly what happens to the objective upon perturbation, not a lower bound (because strong duality holds at $0, 0$).

• Proof

  

Problem Reformulations

A critical important note is that equivalent problem formulations can yield very different duals, which means that reformulations can help if the duals are difficult or too trivial

Common reformulations include

• introduce new variables and equality constraints

• Make explicit constraints implicit, vice versa

• transform objective or constraint functions

Adding new variables and equality constraints

Adding constraints in general can make your dual more interesting. As a very didactic example, if you want to minimize $f_0(Ax + b)$ the dual is constant. Therefore, it helps to introduce a new variable and an equaltiy constraint $y = Ax + b$, which gets you a far more intersting dual.

• Example: $f(Ax + b)$ reformulation

  

• Example: $f(Ax + b)$ where $f$ is a norm

  

Theorems of Alternatives

The Theorem of Alternatives looks at feasibility problems specifically. We look at two systems of inequality/equality constraints. This can be more than one constraint per system.

• A weak alternative is when no more than one system is feasible. This can include the case when neither is feasible.

• A strong alternative is when exactly one of them is feasible all the time. Note that Strong alternatives are necessarily weak alternatives too.

These help because we can implicitly prove that something is not true if you can show that the alternative is true. Or, if you have a strong alternative, you can prove that something is true by showing that the alternative is false.

Weak Alternatives for Feasibility Problems

Recall that we setup a feasibility problem as the objective being $0$. The duality therefore becomes

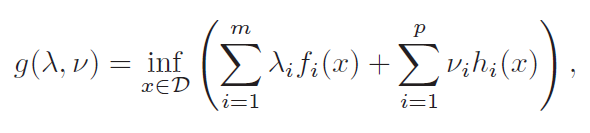
Now this is a really special structure, because $g$ is a homogeneus function of $\lambda, \nu$. Therefore, this is the solution to the dual problem:

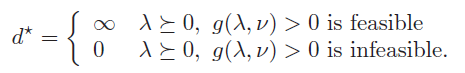
We also know that $d^* \leq p^*$, which means that if $d^*$ is infinite, then the optimal value of the primal problem must be also infinite, meaning that it’s infeasible. Therefore, these two things are weak alternatives:

1. $\lambda \geq 0$, $g(\lambda, \nu) > 0$ is feasible

2. $f_i(x)\leq 0, h_i(x) = 0$ is feasible

If you have strong duality, then (with certain conditions), strong alternatives holds.

Strong alternatives

When the original inequality system is convex, sometimes weak alternatives become strong alternatives. In general, however, you can’t say too much. Don’t assume strong alternativves

• Strong alternative example

  The system $Ax = b, x \geq 0$ does actually have a strong alternative

  

Farka’s Lemma

Farka’s lemma concerns a specific set of nonstrict linear inequalities. The following are strong alternatives:

• Proof: LP duality

  We have the problem and its dual

  

  Strong duality holds, so the feasibilities are linked.

Deriving alternatives

You can derive alternatives by doing the following:

1. Computing dual

2. Find the cases of $\lambda, \nu$ such that $g(\lambda, \nu) > 0$.
   1. Because $g$ is positive homogeneous, we can also write it as $g(\lambda, \nu)\geq 1$.

Because this will tell you that the original problem is not zero, and therefore, it is not feasible

Using alternatives

If you have weak duality and you want to show that something isn’t happening, it is sufficient to show that the alternative is possible (feasible). This can be helpful to plug inti CVXPY.

More specifically: this is an incredibly useful tool! Feasibility problems are “one example” sort of deals. But if you have a set of constraints that you want to be violated (i.e. inverting feasibility), then it is sufficient to find the alternative and show feasibility. Tl;dr it can turn a universal proof into an existence proof.

But importantly, unless you’re given permission to solve a reduced problem, you need strong alternatives to assert that you’re actually solving the same problem

Brief note on dual feasibility

Often when you work on these problems, you take a primal problem → dual problem → feasibility problem. If you take the dual of this again (perhaps to find a strong alternative), you may not get back the primal problem. The dual operation is not subject to the transitive property