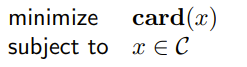Problems involving cardinality

Cardinality problems are basically the number of non-zero components of some $x$. So $card(x)$ would count the number of non-zero components of the vector $x$.

Cardinality is quasiconcave with positive vectors because this holds

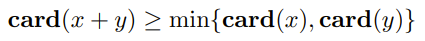
but otherwise there are no other convexity properties. You might be wondering why we even care about this function. Well, it shows up all over the place!

The convex-cardinality problem is a convex problem with some Card(x) inside the problem, either in the objective or the constraint.

Solving Convex-Cardinality

If we fix the sparsity pattern (i.e. the number of non-zero components), it becomes convex. So we could just solve $2^n$ problems and compare. The general convex-cardinality problem is NP hard. Boolean LP, for example, can easily be expressed as a convex-cardinal problem

Other examples of convex-cardinal

• Sparse design: find the sparsest vector that satisfies some specifications

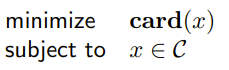
• sparse modeling: explain data with a limited number of regressors; reconstruct signals sparsely

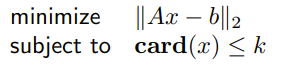
• determining how many inequalities you need to violate (if it’s zero, then it’s a feasibility problem)

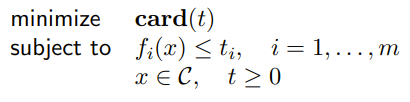
L1 norm heuristic

One way of approach the problem is the replace $card(z)$ with $\gamma ||z||_1$, or add this regularization term to the objective. So you’d transform it like this:

Polishing

We can combine the L1 norm heuristic with the true cardinality objective. First, use L1 objective to find the sparsity pattern. Then, fix this sparsity pattern and solve the original solution.