The big idea

Given $n$ data points, how can we cluster them into $k$ groups?

The intuition is very simple: start out randomly with $k$ centroids $\mu_1, ... \mu_k$. For each $x_i$, assign that $x_i$ to the closest centroid. Then, take all the $x$ that have centroid $\mu_j$ and redefine that centroid to be the center of mass of these $x$'s. Repeat, and you will converge to a proper clustering.

The mathematical expression

This is just the mathematical expression of what we just intuited

Example

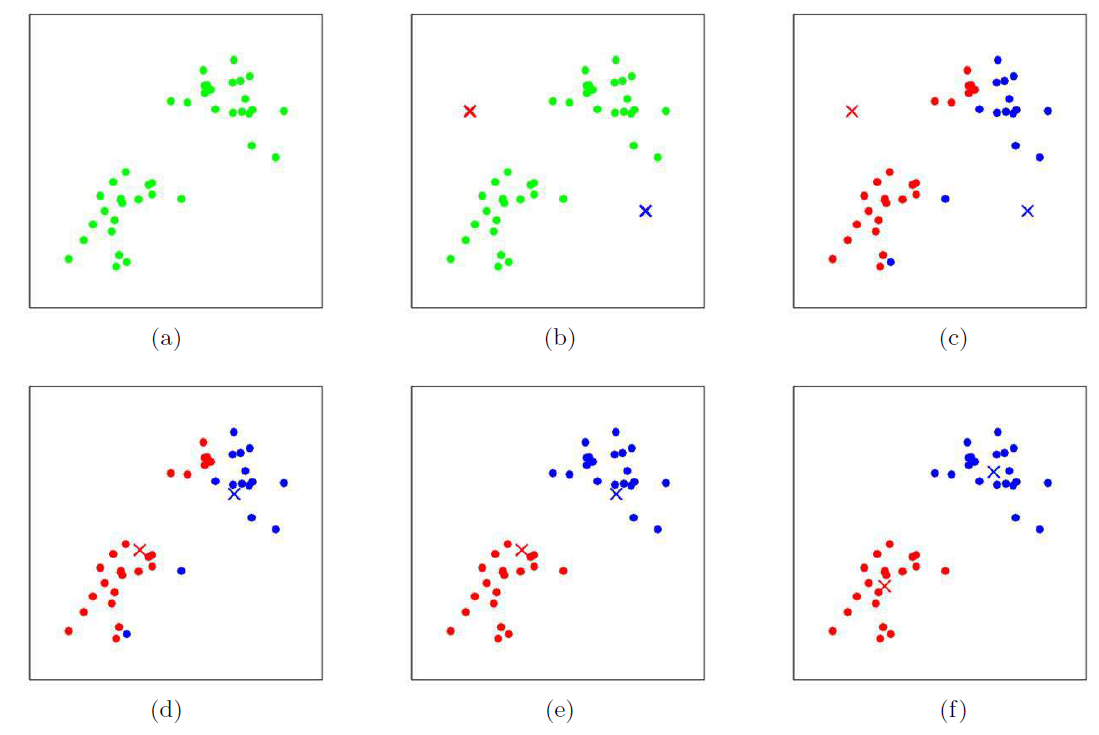
K-means as coordinate descent

We can define the distortion function / potential function as

The optimization is just

When you re-cluster, it's like minimizing $\mu$. When you re-assign clusters, it's like maximizing $c$. As such, you can imagine this whole deal as coordinate descent. We fix one variable, change the other, and then fix the other one, etc.

We are guaranteed to converge. Why? Well, each step you are guaranteed to not get worse: $F(a_t, b_t) \geq F(a_{t+1}, b_t) \geq F(a_{t+1}, b_{t+1})$

However, granted, $J$ is non-convex and there are no convergence guarantees on global minima. To account for this, it's often best to do a few K-means runs with different initializations and pick the one with the lowest converged distortion function loss.

agglomerative clustering

An interesting approach to k-means, known as k-means++, is when you start with a large number of clusters, and then after running k-means for awhile, you cluster the clusters! This allows you to start with high specificity and then move your way down to avoid overfitting.

Limitations

K-means implicitly assumes that your cluster distributions are circular, separable, and have the same size. (the size is because we assign things based on distance from the center).

But these things can come up!

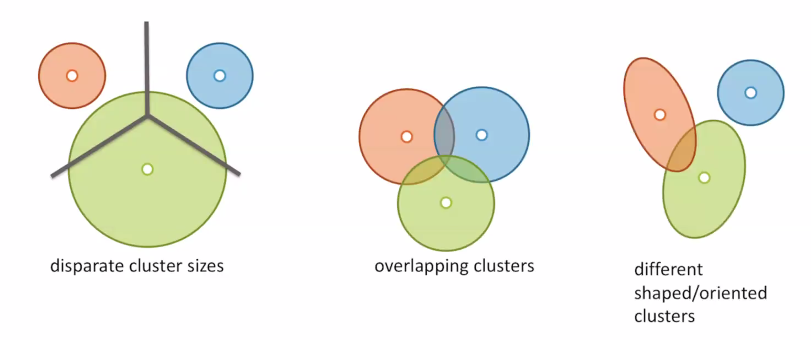
To help us overcome these problems, we resort to a more general class of clustering.