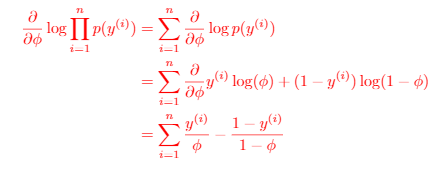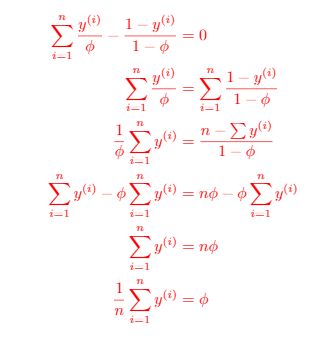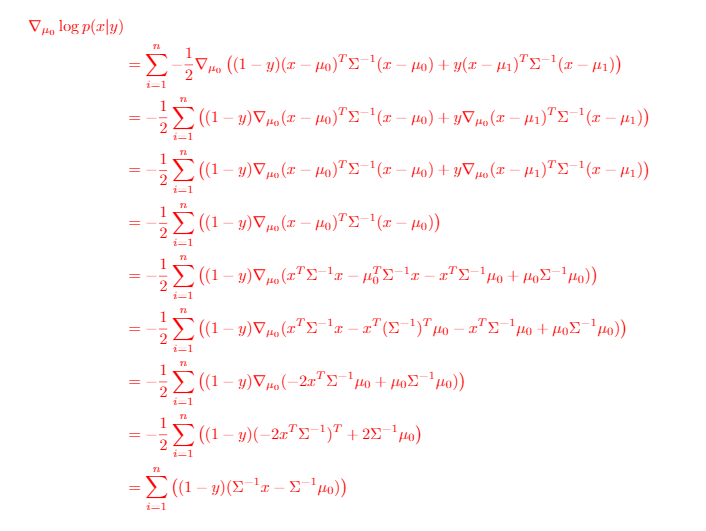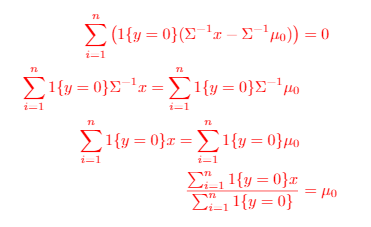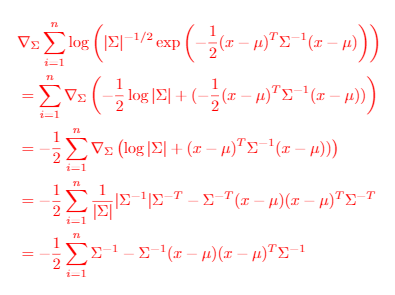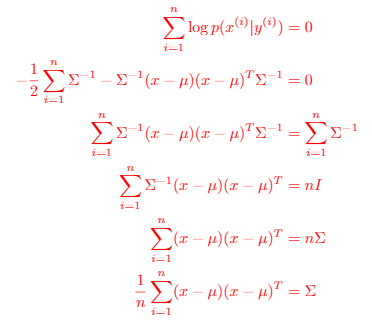Where we are now

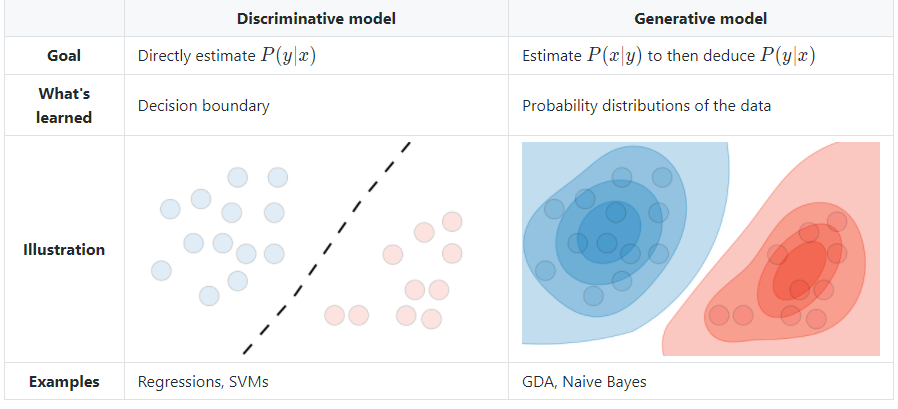
We've talked about algorithms that can model $p(y | x; \theta)$. These are discriminative algorithms. In other words, "given a set of features, predict if it's in one label class".

However, there exists another class of algorithms that are generative algorithms. These model $p(x | y)$ and $p(y)$ and can be used for discrimination indirectly, but they are really doing the task "given a label class, give the expected set of features"

The setup

We need to model $p(y)$, known as the class priors. this is like "what's the probability that this class shows up?" and $p(x | y)$. Then, we use Bayes rule to get what we want

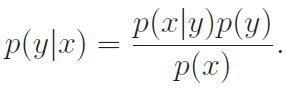
Now, when we are trying to predict which class some $x$ belongs to, we only need the numerator because $p(x)$ doesn't depend on $y$. This helps with our calculations, as we only need relative numbers. However, in the derivations below, we actually use $p(x)$ to be more rigorous.

Gaussian Discriminant Analysis (GDA)

Let $y \sim Ber(\phi)$ (our prior), and let $x | (y = 0) \sim \mathcal{N}(\mu_0, \Sigma)$ and let $x | (y = 1) \sim \mathcal{N}(\mu_1, \Sigma)$.

In other words, we are modeling the features of both classes as gaussians with different means and one shared covariance matrix. The distributions are thus both gaussians of the same shape. Intuitively, it looks like this

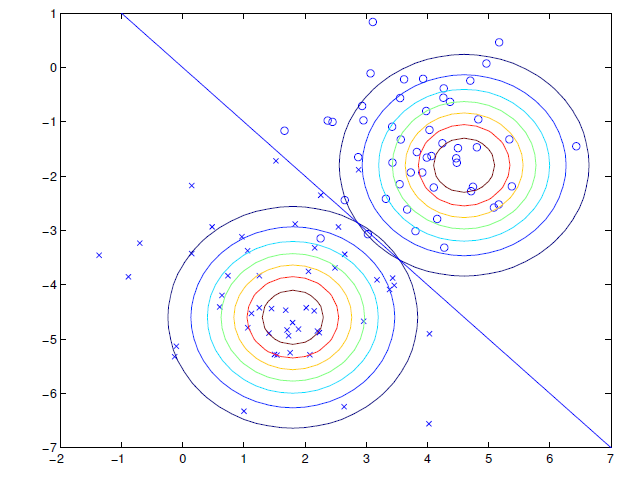
The math

We can write out the distributions like this:

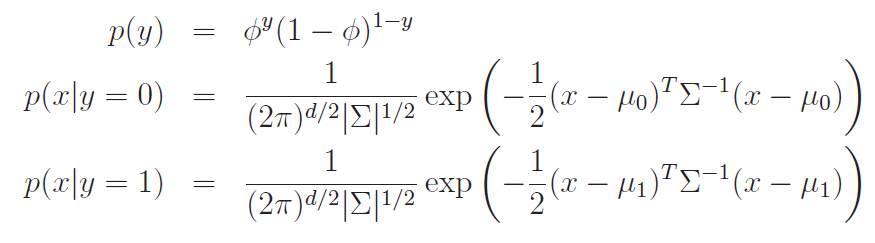
We can define the likelihood function to be just

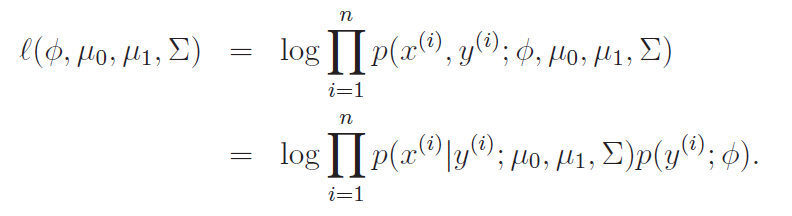
Now, we can derive the MLE as follows

• Derivation of $\phi$

  

  

• Derivation of $\mu$: very messy

  

  

• Derivation of $\Sigma$: very messy but interesting

  

  

Eventually you will get

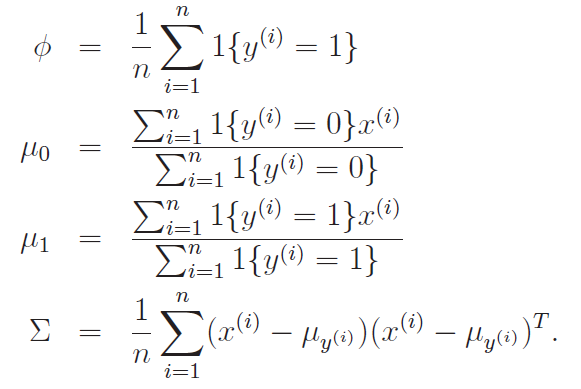
Many of these are intuitive. For example, the $\phi$ prior is just the proportion of $y$, and $\mu_0, \mu_1$ is just the means of the $x$ with $y = 0, y = 1$ respectively. See the derivations above for a more rigorous reason why they are so.

Connection to logistic regression

This is actually really cool. so if you computed the posterior $p(y = 1 | x)$, you will get the logistic regression formula!

• derivation (very messy)

  we want to get $\theta, \theta_0$. In the equation above, the $\theta^Tx$ is replaced with $(\theta^T x+ \theta_0)$

  

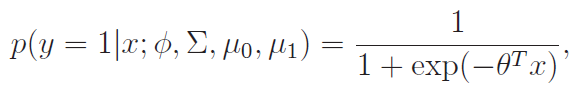
This just means that this generative model is the same as the discriminative model when used in a discrimination context!

Which one do you use?

Well, we have shown that all generative models have logistic posteriors, but it is NOT true that all logistic models have $p(x | y)$ as a gaussian! So the GDA makes stronger assumptions about the data. If $p(x | y)$ is indeed a gaussian then GDA is better. It is asymptotically efficient , which means that there is no better approximation

However, because the logistic makes weaker assumptions, it is more robust. If $p(x | y)$ were from a posison, it can be shown that $p(y|x)$ is also logistic.

If you are sure that the data is non-gaussian, then it is better to not use GDA.

General discussion: discriminative vs generative

Discriminative will try to separate two classes, while generatives will try to model the class distribution and by nature can be converted to a discriminative model through Bayes rule. Generative is therefore more expressive and can do better on smaller datasets as it's always looking for that general model. HOWEVER, generative models require more assumptions. In GDA it was $x | y \sim \mathcal{N}$. Because discriminatives are less expressive, it doesn't need this assumption and therefore can be more robust.

tl;dr

• generative performs better on smaller datasets and can even generate data, but requires significant human design choices

• discriminative is more robust

Good summary chart