The idea

We want to do classification based on a set of discrete and continuous variables. How do we do this without using a neural network?

We use a decision tree!

Measuring accuracy

We can find the accuracy of the current tree by getting the classification error, which is just number wrong / total number

Creating the tree

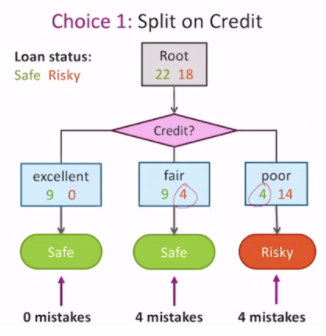
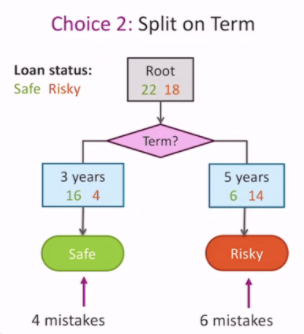
Finding the smallest decision tree that explains all of the data points is an NP-hard problem. Rather, we can be greedy. We start at the root, and we build a decision stump. This stump is how we branch out.

Let's say that we start with $n$ different features. At the root, pick a feature to split on, and then we see what our accuracy is.

We pick the feature that creates the least classification error. This is why it's called a greedy algorithm.

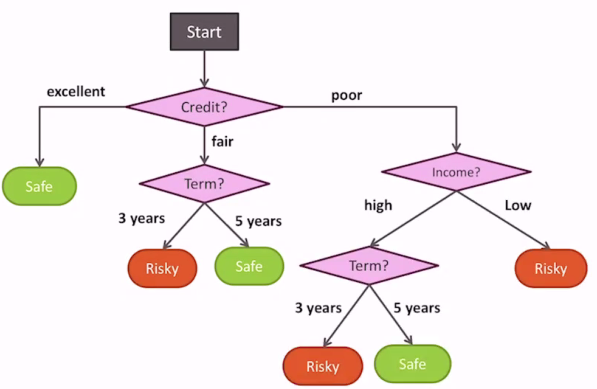
Recursing

Now, on each of these leaves, we look at the number of mistakes. If there are no mistakes, we stop adding to the node. If there still are mistakes, we treat that leaf node as a root and add another decision stump using the same greedy approach we talked about. Once we use a feature, we can't use it again.

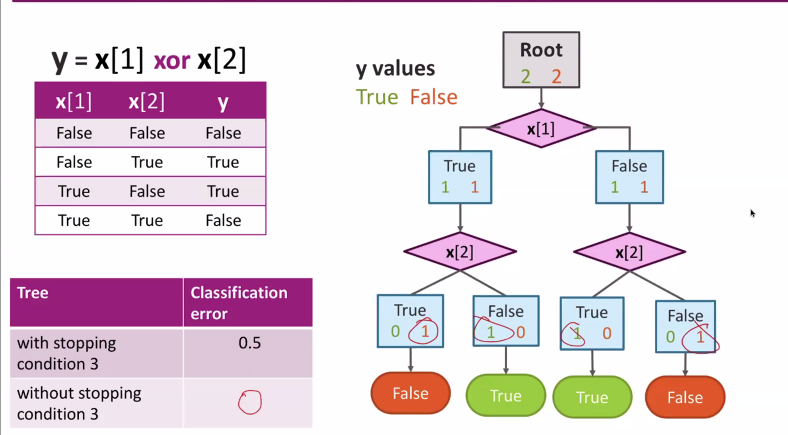
It might seem intuitive that se stop if we have a perfect prediction on the node OR if splitting doesn't decrease the mistakes. However, if we look at an XOR function, we see that this intuition is not always true. Rather, it may seem counterproductive at the current step, but the payoff is in a later split

• XOR example

  

Dividing real numbers

Now, discrete things have been pretty easy to divide. What about real numbers?

Easy! We rely on a binary split, and there are only so many ways of splitting the data

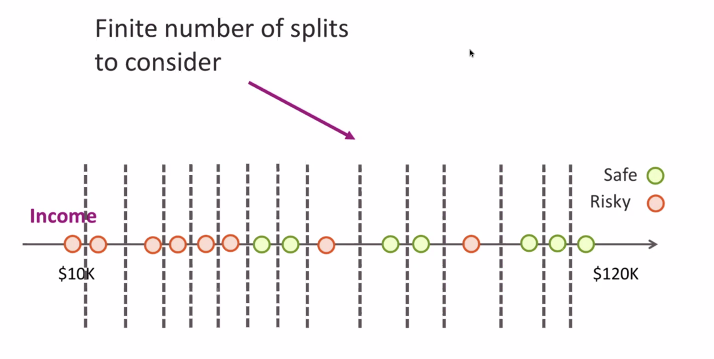
We will pick the split that creates the least mistakes.

Unlike the discrete categories, we can split the same feature multiple times. This is akin to dividing up a space with a razor knife multiple times, like seen below

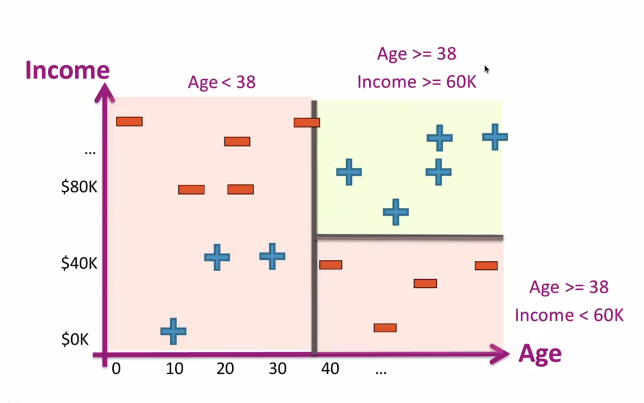
In the simple two-variable design, we can imagine "cornering" each class by making successive horizontal and vertical slices in the data.

Overfitting in decision trees

Continuing with our real-valued decision tree example, we see that if we add more depth to the tree, we get arbitrarily specific boundaries

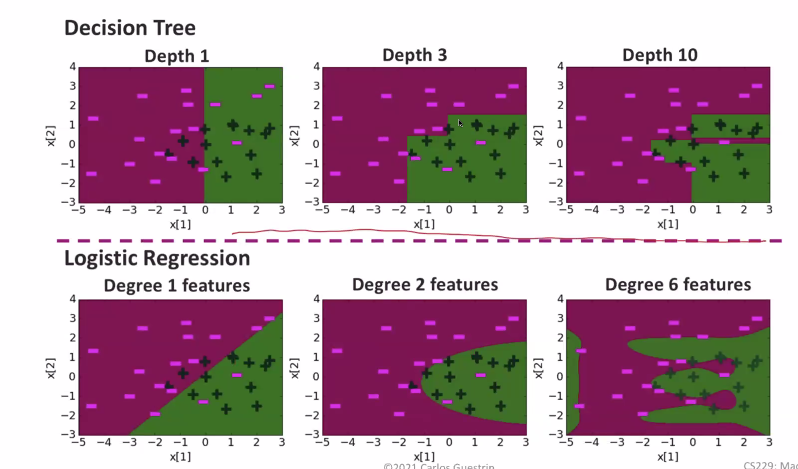
This is akin to defining a complicated kernel in logistic regression, and it can lead to overfitting.

Early stopping

We can fix this overfitting problem by reducing the depth of the search tree, but this is a rather blunt tool.

First, when do we stop? This feels arbitrary

Second, some decisions require greater depth than others. We shouldn't limit all decision to an arbitrary length. So, we arrive at our next (and better) solution

Pruning

The idea is that you start with an overfitted tree (still talking in the continuous splitting tree case) and then you make things smaller.

To do this, we introduce a new loss which is just the

Complexity we define as the number of nodes in tree (NOT the depth, for reasons we just went over).

We start from the lowermost nodes

1. calculate the total loss on the whole tree

2. remove the node and its corresponding leaves

3. calculate the total loss on the modified tree

4. If the new total loss is lower, then we keep our removal decision. Otherwise, replace the node and its corresponding leaves

5. Repeat!

Aside: decision tree regression

Instead of outputting classes, we associate a number with each of the leaves. This is how we can predict numbers instead of classes.