Unsupervised learning

Without an “answer”, you can still do a lot of learning! You can learn some underlying hidden structure of the data. For example, the EM algorithm, dimensionality reduction, etc.

For generative modeling, we want to take in a distribution of training data, and then generate more samples from that same distribution. We can do this in two ways.

1. Explicit density estimation: define $p_{model}(x)$ and then sample from it

2. Implicit density estimation: learn a model that samples $p_{model}(x)$ without actually defining it

Types of Generative models

Tractable density: basically, you take a very complicated density model and somehow make it tractable but exact.

Approximate density: you model the whole thing, but you do it roughly

PixelRNN, PixelCNN

RNN approach

Here, they model the image as a joint distribution across each pixel. To reduce the complexity, they rely on one assumption: the distribution is factorable such that each pixel only depends on the pixels that came before it

This is known as the fully visible belief network (FVBN), and because of the sequential nature, we can just represent the distribution as a RNN rollout. In real life, you can also start generating in a branching sort of way. Note how the arrows point: this indicates dependency

CNN approach

The RNN is too slow, but the idea seems still very interesting. Can we use a CNN? More specifically, let’s use a masked CNN whose output is given to the current pixel, and it is fed back into the next CNN iteration.

The big con here is that it’s still pretty slow...

Variational Autoencoders (VAE)

This time, we are trying to use a latent variable to generate outputs. This of course is intractable, because the computation of the joint distribution $p_\theta(x)$ is defined as

There is no more sequential nature of the pixel generation. However, as we will see in this following derivation, it requires a lower bound optimization. For more information, refer to the 228 notes.

Normal autoencoders

Normal autoencoders shrink down input data into a latent feature embedding $z$, and you train an encoder-decoder together, but you only keep the encoders after training. The autoencoder paradigm is an adaptive way of reducing dimensionality.

The encoder weights can also be a good initialization for a supervised model, especially if you don’t have a lot of data.

So why don’t we modify $z$ and feed it into the decoder? Well, because $z$ is a unknown space. In other words, you create a distribution $p(z)$ when you encode, and the decoder will take $z\sim p(z)$ to output $\hat x$. But because you don’t know $p(z)$, you can’t possibly sample from it, and therefore you can’t mimic the input distribution.

So... why don’t we force a distribution?

Decoder

We assume that the training data is created using some latent distribution $z$. This is a very fair assumption, because let’s say that our trainig data is a bunch of ships. You can imagine $z$ as representing the color, shape, type, etc, of the ships.

Therefore, we want to model this sampling process

To do this, we make one key assumption, which is that the prior $p(z)$ is simple. Note that this does NOT implicate that the image distribution is simple; it just means that the “seed” of the images are generated with regularity. We do this because it simplifies calculations.

Then, we create a $p_\theta(x | z)$, which is a function that maps between latents and the output. This is NOT a simple distribution because the sum of transfomred gaussians is not simple. We model $p_\theta$ through a neural network.

We train the model by attempting to maximize

but this is intractable! You could try a Monte Carlo estimation, but this can be too noisy and not differentiable.

Encoder

You want to essentially make $p(z | x)$, but this is hard! You can try to flip around the decoder, but it requires a marginalization

Why don’t we model this as another function $q_\phi(z | x)$? We can! And more specifically, we let $q_\phi(z|x) = N(\mu_\phi(x), \Sigma_\phi(x))$. The gaussian is important for reasons we will see in a second.

Optimizing the VAE: deriving the lower bound

We will see a variational lower bound derivation. We start with a non-operator, which is taking an expectation across $z$ sampled from $q$

then we expand using bayes rule, and then we do the classical massaging by multiplying by 1

Then, we split things up and recognize the presence of KL divergence

Now, let’s step back a second. The first term can be calculated through Monte Carlo sampling, although we will put a bookmark on this for a hot sec, because sampling isn’t differentiable.

The second term is the KL divergence between two gaussians, which has a closed form solution.

The third term is the KL divergence between a gaussian and a crazy distribution, which does not have a closed form solution. However, KL divergence is always greater than 0, which means that even if we optimize for the first two terms, we will be optimizing a lower bound of the log probabilty.

Logistics in optimization

We want to optimize the lower bound, which is

This is actually very intuitive. We want the model $q$ to output a distribution that is as close to the prior. This is just

which has an analytical derivative. But what about the expectation? Well, as it stands right now, we are trying to take the derivative of $\phi$, which is in the sampler. This can’t work.

But here’s the critical trick. We can sample from $N(\mu_\phi, \Sigma_\phi)$, or we can scale the samples from an identity distribution: $\Sigma_\phi x + \mu_\phi, x \sim N(0, I)$. This is known as the reparameterization trick.

Because you’ve shifted it out of the expectation, the computational graph can be completed like this (and the sampling is part of the gradient now)

What does this look like in full?

You can represent the decoder network as another distribution. The $\mu, \Sigma$ is derived from the $z$, and then the final image is sampled

Now, when you train a VAE, you get some really cool effects. You can “tune” the key features of an image and the network will generate them.

Generative Adversarial Models

Why don’t we just avoid modeling the distribution altogether? Let’s sample random noise, and then transform to the training distribution! But here’s the big problem—it’s not a supervised task, because we don’t know what $z$ corresponds to what training image. So we must be creative!

The game theory

Why don’t we pit two models against each other? The generator maps between noise and the actual image. The discriminator maps between an image and a classification

We call this a min-max objective, because you’re basically playing tug of war, and in doing so, you create two very buff models.

Let’s unpack this. So we want to maximize the probability that the discriminator classifies real data as real, and minimize the probability that the discriminator classifies fake data as real. However, in the same objective, we want to change the generator such that the discriminator classifies this data as high as possible.

The algorithm

We just alternate between two gradient descents

Tips of the trade

It takes a long time to fool the discriminator, so the generator starts out at a relatively flat point in the gradient. This is the nature of the $\log 1 - D$ signal.

To fix this, we just flip the objective and perform gradient asscent on the following

This leads to the following terrain

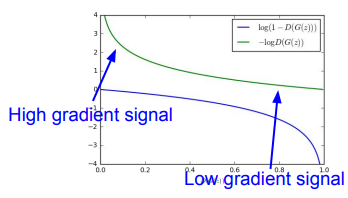
You update the discriminator $k$ steps for every step you update the generator. Some people use $k=1$, other people use greater than 1.

For stable GANs:

Cool things about GANS

Because you’re essentially making a continuous function, if you have two latent vectors, you can generate a “gradient” between the vectors, which translates to large changes in the environments

You can even do vector addition and subtraction to “remove” a feature.

You can do style transfer (cycleGAN), and even image synthesis.