Explicit Representations

There are non-parametric (points, meshes) and parametric representations.

Point clouds (non-parametric)

This is the simplest representations. You just have a set of points. You might have a normal vector, which allows you to approximate the points as disks. this is used for shading. These disks are known as surfels.

Depth cameras capture point clouds. The problem is that it’s potentially noisy, and it relies on sampling. On undersampled regions, it’s hard to understand. And it’s hard to simplify (scale down) or subdivide (scale up). And lastly, there’s no topological information. What parts are open or closed?

Voxels (non-parametric)

Basically, you get a spatial grid of points, and you either set the point to “true” if there is an object part in that voxel, and “false” if there isn’t an object part. Below we have the natural rabbit, and on the right, the voxel rabbit

Meshes (non-parametric)

You represent the surface as a bunch of connected polygons. You can easily increase resolution through interpolation, and decrease resolution through mesh simplification. You can also regularize the mesh (make more even-sized shapes) to improve the quality.

A mesh consists of vertices, edges, and faces. Each simple polygon formed by the vertices and edges is a face. The boundary of the mesh is either empty (if the mesh is closed) or forms closed loops.

You can make any polygonal mesh into a triangular mesh. This is particularly helpful because modern graphics processors specialize in triangular operations. Furthermore, unlike polygons which may not be planar, all triangles are planar.

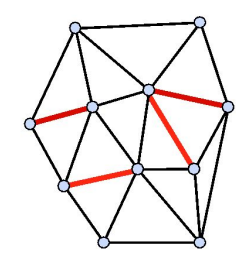
To store, just keep track of each vertex and keep track of the vertices that correspond to each triangle.

Parametric representations

Basically, you represent a shape through a parameters and a “sweeping” variable set.

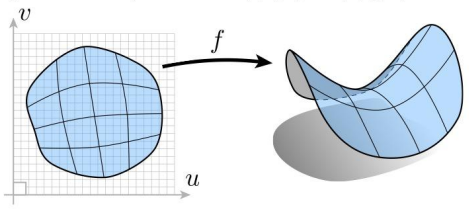
One example is UV projections. Basically, you define a parametric surface $\langle x(u, v), y(u,v), z(u, v)\rangle$ that is a function of $u, v$ that you sweep across.

Another example is bezier curves, which can be extrapolated to patches through a tensor product.

It’s easy to sample from this surface; just sample in u-v space and project it! However, it’s harder to tell if a point is inside or outside a region. What we’re getting at is that some tasks are hard with explicit representations.

Implicit representations

Point classification

You can define a function $f(x, y, z)$. The surface $f(x, y, z) = 0$ is an implicit shape, and you can imagine $f$ as a classifier that separates positive and negative values.

A classical example is the sphere: $x^2 + y^2 + z^2 = 1$.

It’s hard to sample from this representation, but it is almost trivial to tell which side a point is on, because $f$ is literally a classifier for it!

Algebraic surfaces

The sphere is an algebraic surface , and more specifically, a sphere is the zero-set of $x^2 + y^2 + z^2 - 1$. So, again, it’s very much like point classification.

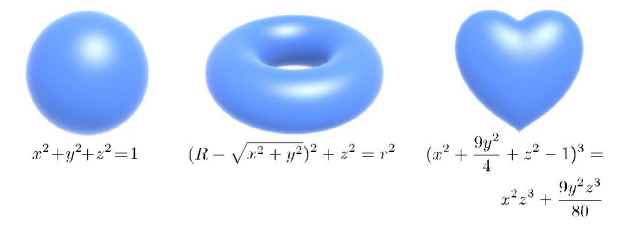
Because these are constraints, you can imagine welding them together through boolean operations

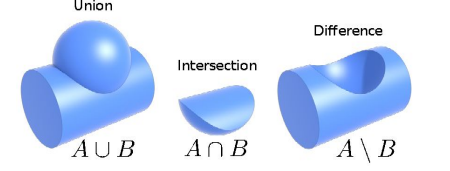
and this allows you to get some fairly complicated figures

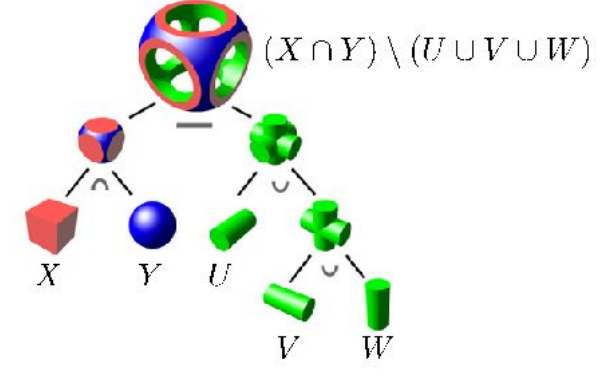
and instead of Booleans, you can maybe even combine constraints using softer distance functions

Level set methods

Often, it’s hard to express complicated shapes in closed form, even with the power of boolean composition. Instead, we can just represent the function as a grid of numbers and then draw a line manually

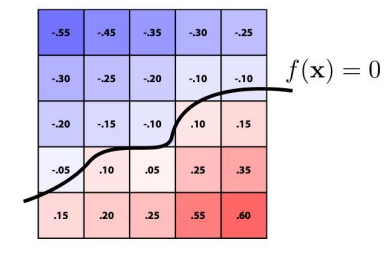
You do this across depth slices. This is how medical people do imagery like tomography.

Using AI in 3d vision

There are a ton of datasets for 3d vision, including Pascal 3D+, ScanNet, igibson, etc. Here are some applications

• generate new shapes

• classify shapes

• render shapes

Multi-view representations

We can just give a lot of views to a 2d CNN, and then pool the views together, run it through a softmax, and get a prediction.

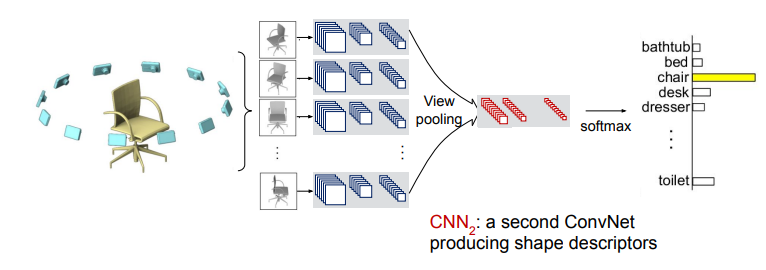
these are good because you can use pretrained features from things like ImageNet. The downside is that you need to get all of these camera angles, which is not trivial . Noise can also be a problem

Voxel inference

You can just perform 3d convolution on a voxel field, which is known as a deep belief network (CDBN). The filters actually learn some useful lower-level voxel types

Other voxel applications

You can have a volumetric autoencoder, which allows for self-supervisino. We can use a 3D-GAN, although it is quite finicky. You can also use GANs to add texture

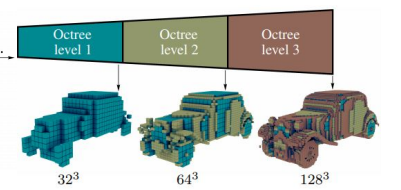
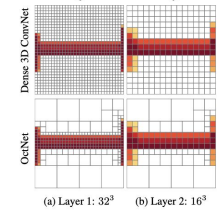
Now, voxels can be a bad waste of space because we only really care about the immediate region surrounding the objects. The size of the empty areas don’t matter, so why don’t we reduce the granularity of that space? Here, we arrive at Octree, which recursively partitions a 3d space.

With the hierarchical structure, you can also build up a model with incremental degrees of precision

Point Clouds and Pointnet

pointnet will take in a set of points to do a variety of tasks down the line. The difficulty of points is that

1) The order of the points shouldn’t change the outcome

2) Our output should depend on the underlying geometry, not the sampling luck.

So you can’t just easily to MSE. But there are some tricks up our sleeve.

A good way is to use Chamfer distance, which compares a set of generated points with the set of ground truth points. They match each point with its closest peaks.

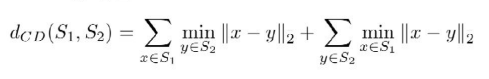
This makes it insensitive to sampling, at least relatively.

Point Clouds and convolutions

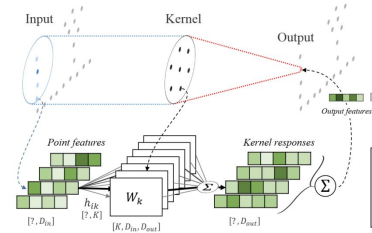
If you represented point clouds as graphs whose edges represent relationship between neighbors, we can run a message-passing Graph neural network, which means that can propagate dependencies through a network this size.

We might also use Kernel Point Convolutions (KPConv), which use a graph as filters.

Mesh generation

You can start with a ellipsoid mesh and then slowly extract features from an image and use that to iteratively modify the ellipsoid.

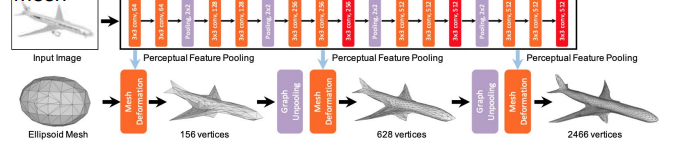
You can also add an option to “cut” the surface to change the topology, which allows for greater expressivity.

Parametric decoder

People realized that MLPs were great at function approximation. So why can’t we approximate the unrolling of a U-V map? That’s the goal of atlasnet,.

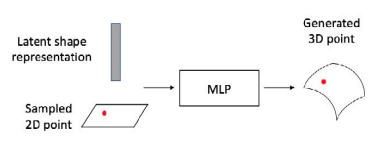
From this you can also try folding or assembling primitives.

Implicit functions

So, people also realized that neural networks are great at discriminating things. So why don’t we make a neural network $f$ that implicitly represents a shape through its decision shape?

You can apply this to the voxels directly, which output a 1 if there is a point there, or a 0 if there is a not. You can imagine scaling this up to include color and transparency. This brings us to Neural Radience Fields, which integrates the luminance and transparency along a camera ray to get the observed color.