Grade school multiplication

In grade school multiplication, we multiply together $n^2$ numbers (think about it). Can we do better?

Divide and conquer: a start

For some number of magnitude $10^n$, given that $n$ is even, we can split it up like this:

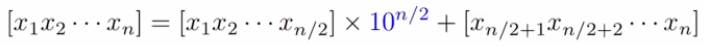
And this means that multiplication becomes

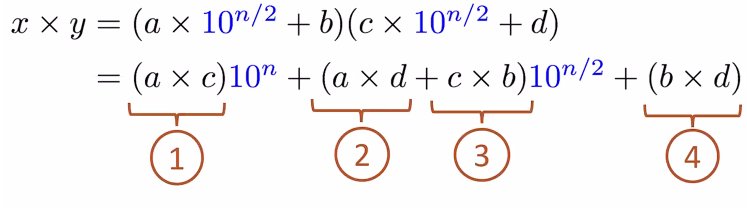
The key insight is that a one n-digit multiplication can be written in terms of 4 $\frac{n}{2}$ digit multiplications!

Recursing

You can think of a very simple recursive algorithm that uses this insight. The base case is when $n = 1$, in which you compute a one-digit product.

We assume that $n$ is a power of 2 to help us. If $n$ is not a power of 2, we need to augment the splitting somehow. Here’s the insight: instead of worrying about if $n$ is even or not, we focus on if the two numbers are of the same size. If they are not the same size (which will happen when $n$ is odd and you split), you pad the numbers with leading zeros until they are of the same size. Now, this size could be even or odd. If they are even, then the next cycle will get a clean split. If they are odd, the next cycle might get a bad split but more padding will fix it.

Why does this work? Well, leading zeros do not change the properties of the numbers. Some of the base cases will involve multiplying numbers by zero, which does waste computational resources but it makes the problem feasible.

Does this help us?

Well, here’s some facts. Every step, we reduce the problem by half. We also increase the number of problems by 4. Therefore, at the end we reduce by $t = \log_2(n)$ times, but we increase the number of problems by $4^t = 4^{\log_2(n)}$ times, which is equivalent to $n^2$. Hmmm.

It actually appears that we’ve done all this work for nothing! But we haven’t made zero progress. The key insight is that we are only stuck because the branch factor is 4. Can we reduce this number?

Karatsuba algorithm

Here’s the key insight. We need to recurse on 3 problems instead of 4. To do this, we compute (using our previous terminology) $a*c, b*d, (a + b)*(c + d)$. The general approahc is to break it up into 9 n/3 sized problems, and then find 5 distinctive products of n/3 such that you can generate the 9 n/3 products through subtraction and addition. It’s a fun little puzzle.

This is because $(a+b)(c+d) = ac + bd + bc + ad$, and we need $ad + bc$. Therefore, we can just compute $(a+b)(c + d) - ac - bd$ to get this term. And $ac, bd$ are used in the other two parts of the expansion. So we do indeed only compute three multiplication operations!

And this gets us $3^{\log_2(n)}$, which is equivalent to $n^{log_2(3)}$, which is around $n^{1.6}$. This is a lower order!

Other approaches

Toom-Cook proposed an algorithm that breaks something into five n/3-sized problems, which yields a complexity of $n^{\log_3(5)} = n^{1.46}$.

Schonhate-Strassen in 1971 proposed an algorithm that runs in $O(n \log(n)\log\log(n))$ time.

Furer in 2007 propsoed an algorithm that runs in $n\log(n)* 2^{O(\log^*(n))}$

Harvey and van der Hoeven in 2019 proposed an algorithm that runs in $O(n \log(n))$ time.