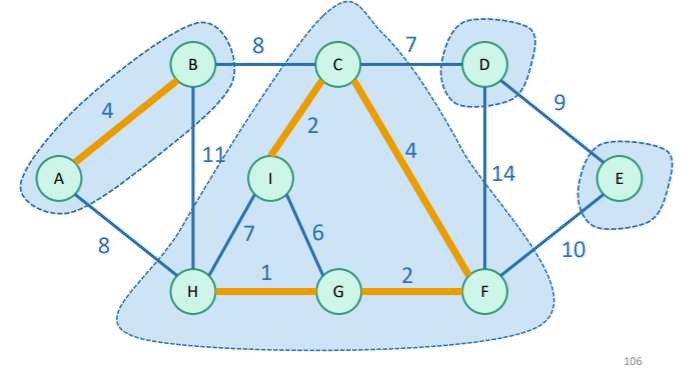
Minimum Spanning Tree

Given an undirected weighted graph, a minimum spanning tree is the same graph with a subset of edges such that the graph is now a tree (no cycles) with edges whose sum is minimized.

It has uses in many fields, including network design, cluster analysis, image processing, and as a useful primitive for other graph algorithms. We saw in 228 that the Chow Liu algorithm uses an MST.

To find an MST, we want to use a greedy algorithm. However, before we do this, we need to talk about cuts.

Cuts

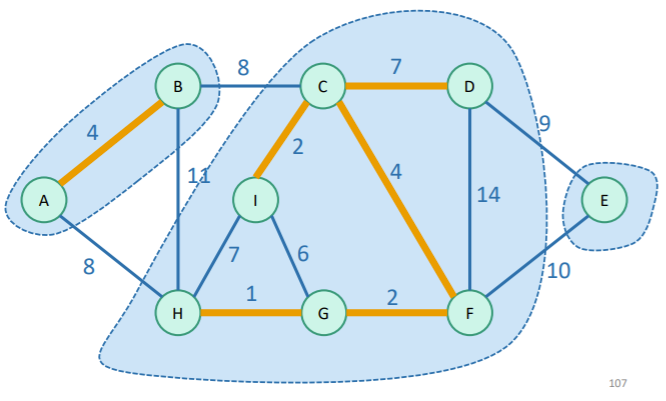
A cut in a graph is a partition of vertices into two parts. If you represented the graph with nodes and strings, a cut would literally be cutting the strings to separate the nodes out.

Now, you can make multiple “cuts”. The goal here isn’t to have two connected components. The goal is to separate the vertices into two bins.

Light edges and respectful cuts

Let $S$ be a set of edges in a graph $G$. A cut respects $S$ if no edges in $S$ cross the cut. In other words, the scissors don’t cut the string that representst hat edge.

Equivalently, we can think of each connected graph component described by $S$ as being on one side only

An edge that crosses the cut (i.e. one that gets cut) us called light if it’s the smallest weight of any edge crossing the cut. There can be more than one light edges if weights are the same

Key lemma

Let $S$ be a set of edges, and let there be some cut that respects $S$. Suppose that there is an MST that contains $S$, and let $\{u, v\}$ be a light edge. Then, we can claim that there is an MST that has $S \cup \{u, v\}$. Now, we now that “some cut” is a universal statement, which means that essentially if you draw a cut, the light edge must be included in the final MST, regardless of what cut you make s

Let’s try to prove this. If we have a cut that respects $S$, then we have something like this

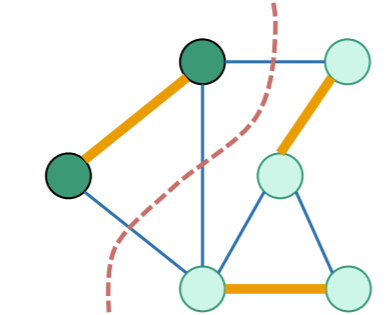
Now, this is sort of confusing because both sides contain $S$. That’s fine, because when we make our MST assumption, then it is necessary that one of the sides is a connected component. Think about that for a second. Because we are trying to extend an MST.

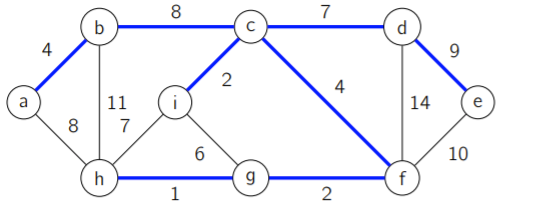
Let’s start from an optimal MST $T$ that connects all the components together (highlighted in yellow)

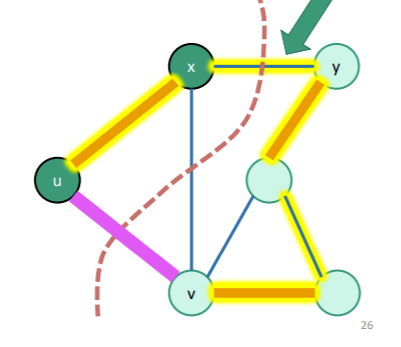
If $\{u, v\} \in T$, then we are done. But in the example above, this is clearly not the case. But suppose that the crossing edge was $\{x, y\}$. We know that $x, u$ are connected because it’s a tree $T$.

We claim that we can switch out $\{x, y\}$ for $\{u, v\}$ and still keep optimality. This is because $\{u, v\}$ has at most the weight of $\{x, y\}$ (by the light edge definition), but we also claim that $\{u, v\}$ has at least the weight of $\{x, y\}$ or else $T$ is not an MST. Therefore, we arrive at the restriction that the two edges must have the same weight. And because $u$ is connected to $x$, and because $v$ is connected to $y$, switching the edges doesn’t change anything about the connectivity.

Let’s repeat that for a second. The edge $x→y$ is the only edge that connects the components across the wall. If we added another edge across the wall, then we would form a cycle (see tree definition)

The key upshot: starting from some $S$ and drawing a cut that respects $S$, it is possible to create an MST that contains the light edge .

Another side upshot: the minimum weight edge on every vertex must be part of an MST, because you can just draw a cut along that edge and that would be the light edge.

Prim’s algorithm

This is a very simple greedy algorithm that builds up an MST. Just add the shortest edge that can grow the tree. In other words, find an unconnected vertex that we can get there in the least cost from our current set of connected vertices.

Naive implementation

Essentially, keep a set of visited vertices and unvisited vertices. For every step, look through every edge of the graph and pick the edge that has one vertex in the visited set and another vertex in the unvisited set.

This has complexity $O(nm)$, which isn’t the best. If we are dealing with a densely connected network, we have complexity $O(n^3)$.

• Implementation

  

Proof of correctness

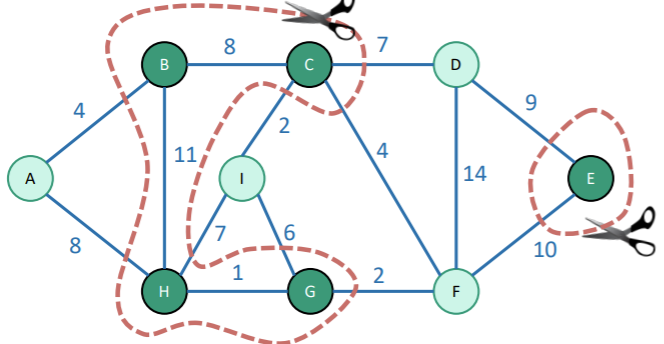
Let’s say that we have already added edges $S$ to the graph. Now, we perform a cut that respects $S$. We suppose that there is an MST that includes all edges in $S$. Now, because $S$ forms a tree, the cut will separate out a connected component from the non-visited components.

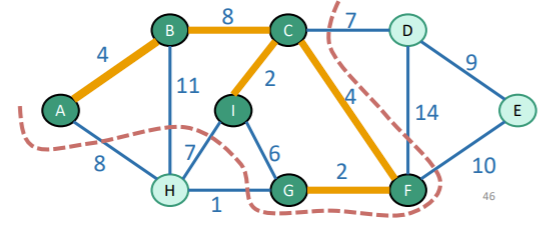
From this, we note that Prim’s algorithm will pick the light edge and add one edge to $S$. From the cutting lemma, we conclude that adding this edge still keeps the MST optimal.

Implementing this in a more efficient way

Previously, we had a pretty naive implementation that had pretty bad time complexity. Can we do better?

Actually, yes! We can just take inspiration from Djikstra’s algorithm. We keep track of $d[v]$, where $d[v]$ is the distance of $v$ from the growing tree. If none of the neighbors are in the tree, then $d[v] = \infty$.

At each step, you add a node, and then you update its neighbors $v’$ such that $d[v’] = \min(d[v'],w(v, v’))$

This is slightly different from Djikstra, whose $d[v]$ is the distance of node $v$ to source $s$.

However, in both algorithms, you use a priority queue to pick the vertex that has the smallest distance from the tree, because that’s exactly the edge you want to select!

• Pseudocode

  

New runtime

Because this is basically Djikstras with a small modification to the update formula, it has the same complexity. We select the smallest element, and then enqueue. Using a Fibonacci heap, we can get $O(m + n\log n)$. See notes on Djikstras for more information.

Kruskal’s Algorithm

This one is another greedy algorithm, and it revolves adding the smallest edge that doesn’t create a cycle. To do this, you need to run a BFS from one of the vertices you plan to add and edge to, and if you don’t come up with the other vertex, then you’re good.

Naive implementation

The easiest way is to have a set of visited nodes. Then, in every step, you pick the edge whose corresponding vertices are NOT both in the set of visited nodes. If you add an edge like this, then you will create a cycle. You stop when all edges have corresponding vertices in the set of visited nodes.

Unfortunately, while this is correct, you have complexity $O(nm)$ again, and that’s no good.

Smarter implementation

At every step of the algorithm, we have a forest (of trees).

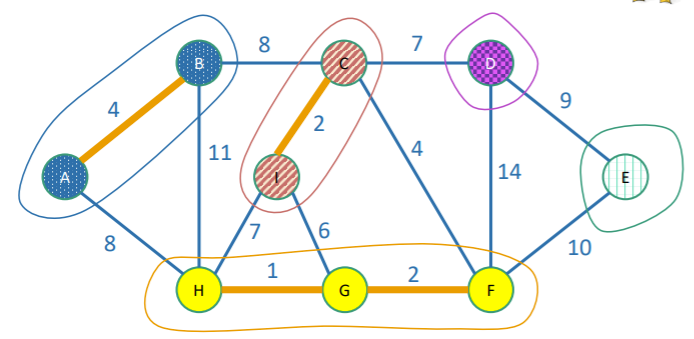
A singular vertex is also a tree. So with this definition, every time we add an edge, we merge two trees. So a good way of implementing this algorithm is to store each tree in a datastructure, and as we add edges, we just merge the trees that belong on either side of the edge (given that you make sure that the edge doesn’t connect the same tree to itself). The key part is that both traversed and non-traversed edges are included in a tree object, as the tree object looks at the vertices involved. So unlike the naive solution, we don’t even consider trying some of the edges.

• Example (one step)

  

  

• Implementation (pseudocode)

  The find will get the index of the forest that the vertices are in

  

Run time

We need to sort the edges, which takes $O(m\log n)$ time. (it’s $O(m\log n^2)$, which is just $O(m \log n)$. We can potentially use a radix sort to get $O(m)$

1. we need to make a set $n$ times (put each vertex into its own tree set at the beginning)

2. call $2m$ finds, because for each edge you add, you find its endpoints.

3. call $n-1$ unions, because every edge you add will require a union, and there are $n-1$ edges in the MST

For all intents and purposes, the finding and the union can take place in $O(1)$ time, and we know that $n < m$, so the final complexity is $O(m \log n)$.

If we use radix sort, then we get the complexity as $O(m + n)$, which is just $O(m)$ on a connected graph.

Proof of correctness

Every step we will merge two trees, $T1, T2$. We can make the cut that separates the vercies into $T1, V- T1$. By Kruskal’s algorithm we always add the smallest edge between the two because we sort the edges by their increasing weight.

By the cutting lemma, we are creating a light edge and have some $S$, which means that indeed, there should still exist an optimal MST, as desired.

Which one do I use?

The Prim will grow a tree in $O(m + n\log n)$ with a Fibonacci heap. With denser graphs, where $m \approx n^2$, this might be the better bet because it becomes $O(n^2)$.

Kruskal grows a forest, and if the weights are small integers and you can do Radix sort, it becomes $O(m)$ (from $O(m\log n)$. However, if the weights are continuous and $m\approx n^2$, now you’ve got $O(n^2 \log n)$, which is a little slower than Prim.

Prim’s algorithm must have a starting node, while Kruskal begins anywhere

More examples

The key insight: the air is just another city with connections to all other cities, with cost $a_i$!!

1. Try making no airports. In other words, don’t add the air node and then run MST. This is key, because if you add the air node, you are implying that at least two airports be built, which may not be true

2. Try adding the air node in and then running another MST.

3. pick the MST that has the lower cost.