The motivation

What if we wanted to find all pairwise shortest path? (APSP)?

We can use $n$ Bellman-Ford steps, which takes $n^2m$ complexity. If there are no negative edges, we can use $n$ steps of djikstra’s algorithm, which takes $n^2\log n + nm$.

If $m \propto n^2$, then BF takes $n^4$ complexity, and Djikstra takes $n^2\log n + n^3$, which is OK but can we just do it in $O(n^3)$ steps, regardless of edge weight sign?

Implementation

Substructure

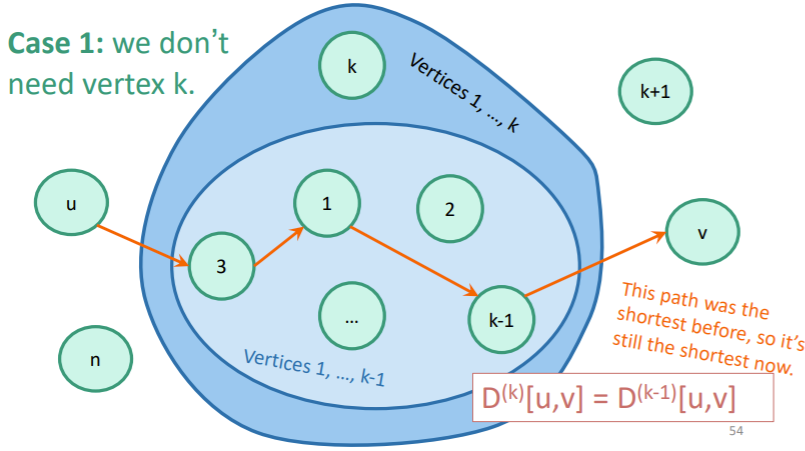
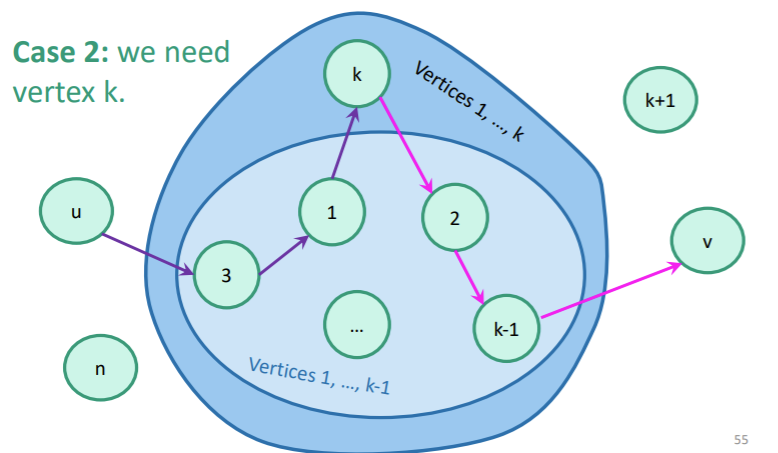
Here, we put on our dynamic programming thinking caps. What sort of subproblem can we design? How about an array $D^{(k)}[i, j]$ that is the shortest path between $i, j$ such that all the vertices between $i, j$ are vertices $1, ... k$.

This actually a little bit counterintuitive. The knee-jerk adaptation is to use bellman-ford but pairwise. In that case, $D$ would be the shortest path such that the number of vertices between $i, j$ are less than $k$. However, you can show to yourself that this yields $O(n^4)$ complexity and is not good.

What happens at each step

You would initialize $D^{(0)}$ as the weighted adjacency matrix (and non-edges are infinite). This because direct edges have no vertices between them, which satisfies the definition of $D$. Then, you would do the following:

1. Select a pair of nodes $A, C$ (represented as an element in $D$).

2. Try if $A→k→C$ is of lower weight than $A→C$. If you can find one, update the distance in $D$. If not, keep what you have. You can use $A→k$ and $k→C$ as defined in your $D$.

Inductively, it should be easy to show that you keep the inductive definition of $D$ after doing this step.

Much like Bellman-Ford, you can show that you only need $n-1$ steps to complete. In each step, you iterate through $n^2$ pairs of vertices, yielding a final complexity of $O(n^3)$.

• Graphical explanation

  

  

Algorithm box

Detecting negative cycles

If there are negative cycles, then $D[v, v] < 0$. Because negative cycles necessairly mean that you can circle back to where you started and be better off.