Motivation

Suppose that we wanted to find the shortest path in a graph that had weights. What do we do?

Well, there’s a really dumb way of doing it. We just connect the nodes with lengths of string that are proportional to the values of the edge weights, and then lift the root slowly.

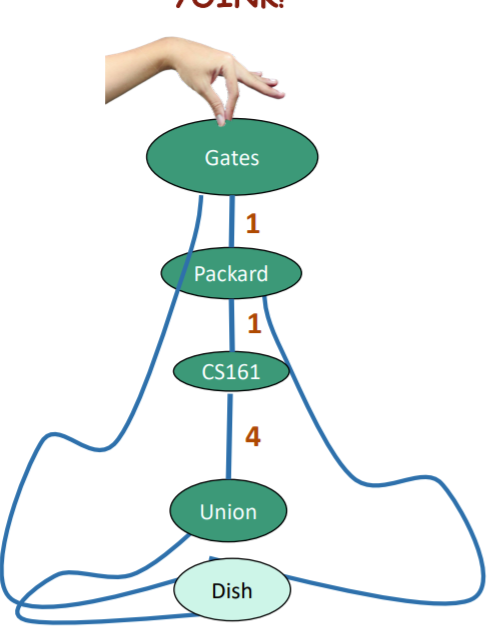
The reason why this works is because the string forces a shortest weighted path. But this is kinda dumb because we don’t really gain any algorithmic insight. Can we do better?

The algorithm

Let’s talk about it informally and then we will give the proof.

1. Store a distance from the source node $s$ in each node. This is always an overestimate of the true distance, so we initialize all of them to infinity. We will denote this as $d[u]$. We know that $d'[u] \geq d(s, u)$

2. take the node $u$ with the smallest distance measurement (you might use something like a heap; we’ll talk later), and then update all of its neighbors $v$ using this formula:

(where $e_{u, v}$ is the edge weight between $u, v$.)

Why? Well, we can say that $d[v]$ is the length of the shortest current path, but if coming from $u$ proposes something better, we update this value to reflect this change.

3. When we are done enumerating all the neighbors, we mark the $u$ as complete.

The algorithm box

Here, the $F$ is the set of nodes to explore, and the $D$ is the set of nodes that we are done with. Note that it’s not obvious why when we are done exploring a node, its distance doesn’t get updated again. We will look at the formalism below

Why does it work?

Theorem: at the end of the algorithm, $d[v]$ is the actual distance $d(s, v)$ .

To prove this, we prove two claims

1. for all $v$, $d[v] \geq d(s, v)$

2. when a vertex is done exploring, $d[v] = d(s, v)$

This proves the theorem because we know that once we are done exploring, we hit this value from (1), we know that it never goes beyond. Whats more, all vertices are done exploring at the end.

Lemma 1

If we have a shortest path from $s → u$ and $v$ lies on that path, then this is also the shortest path from $s→v$.

we prove this by contradiction. If there exists a shorter path between $s→v$, then we can just swap out the $s→v$ subpath in the original $s→u$ to form a shorter path. But this is a contradiction because we’ve established that the original $s→u$ is the shortest path.

Claim 1

This is basically saying that we are always over-estimating. This is pretty obvious from the equation

again, we understand that $d[v]$ is the length of the path we have in mind, which is obviously at most the length of the shortest path.

Claim 2

This is more nuanced. We will show this by induction

• Hypothesis: when we mark the ith vertex $v$ as done, $d[v] = d(s, v)$

• Base case: the first vertex marked done is the $s$, and $d[s] = d(s, s) = 0$ as desired

Now, the inductive step. Suppose that we just added $v$ to the “done” pile, and we are just about to add $u$ to the done list. We want to show that $d[u] = d(s, u)$. We will use the term good to refer to when this situation is true.

We want to show that $u$ is good. Let’s do this by contradiction. Consider the true shortest path to $u$. Let $z$ be the last vertex that is good, where $z \neq u$. Let $z’$ be the node after $z$, which can be $u$ but doesn’t have to be

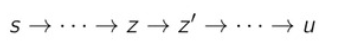
Now, what can we say about this whole thing? Well, because $z$ is good, we know that

Because $z$ is on the path to $u$, it must be the case that

Now, as we have previously claimed, $u$ is not good, which means that

From all of this and the knowledge that $u$ is not good , we know that, $d[z] < d[u]$.

We also know, because we picked the $u$ such that $d[u]$ was the smallest and because $d[z] < d[u]$, then $z$ MUST be done! (i.e. not up for grabs anymore).

But then, if $z$ is done, then we’ve already updated $z’$ by the rules of

(the second part of the equality comes from the subpath thing). If there were a shorter path from $s$ to $z’$ other than $s→z→z’$, then $d(s, z)$ would have to be shorter.

However, by claim (1), we know that $d[z’] \geq d(s, z’)$. As such, we are forced to conclude that $d[z’] = d(s, z’)$. What does that tell us? It tells us that $z’$ is good. And this is a contradiction to what we originally claimed, which is that $z$ is the farthest good node, which completes the proof by contradiction

This is a general framework of the proof

1. assume that $z$ is good

2. show that it must be done

3. show that $z’$ must be good as well, which is a contradiction

Where do you start?

If the graph is SCC, then after running Djikstra’s algorithm, we will get the minimum distance between the source and all the other vertices

However, if the graph is not SCC, you will get the information for a subset of the nodes. At the end of the day, Djikstra computes the shortest distance from a source node $s$, and the choice of source node can really influence the distance (and even if you are able to reach certain nodes on directed graphs.)

How fast is it?

Well, let’s think about the algorihtm in general. We needto

1. Find the minimum value of a map of numbers

2. Remove the minimum value of a map of numbers

3. Update the key-value pair of a map of numbers

More specifically, we need to peel off the vertices by its minimum value, so if there are $n$ vertices and $m$ edges, we need to find/remove the minimum $n$ times, and update the key $m$ times. This because for every edge, we will be propagating some message down it

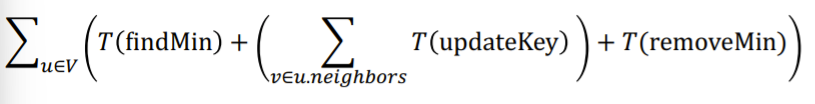
Proposed structures

If we use an array, then our final complexity is

If we us a RB tree, we get

IF we use a heap, we can have similar performance

If we use a Fibonacci heap, we can actually insert insert, find minimum, decrease key in $O(1)$ time and delete the minimum in $O(\log n)$ “amortized” time, meaning that things happen over successive calls to these operations. In this case, the total runtime is $O(m + n\log n)$

What’s wrong with Dijkstra?

It can’t handle negative edge weights. Why? Well, it makes one key assumption: when you pick a node $X$, it means that this node is the smallest distance from the source. it also means that it is impossible to make it shorter, as there are no shorter nodes to expand from. Therefore, after you explore its neighbors, you “lock” $X$.

While this is very true for positive weights, it is not true for negative weights. It may be possible that a current node $Y$ has a higher distance but it has a negative edge between $Y$ and $X$, which may make the final distance of $X$ smaller.

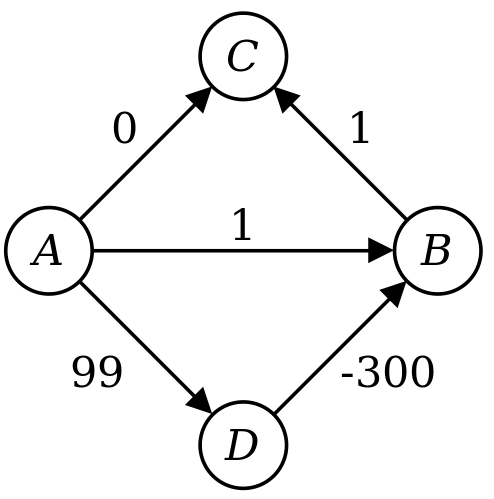
Feel free to trace through Dijkstra’s algorithm on the graph below, starting at $A$. You will see that $C$ gets too high of a final distance.

Challenge question

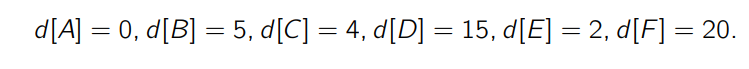
If we know that the algorithm is currently on $C$, what can we tell about the upper and lower bounds of the true distance from $A$? Well, we know the upper bounds from the $d$. But what about the lower bounds?

• We know that $E$ is done because if we are on a value of 4, then a value of 2 must have been excluded.

• We also know that $C$ is the closest to $A$

• Therefore, anything that goes down must be connected to $C$, which means that all the nodes have a lower bound of $4$.

This was very tricky reasoning!

Challenge question part 2

Basically, the algorithm modification is as follows: instead of picking the $d$ with the smallest value, pick the lowest $C$ that is still not “done”, and then pick the $d$ within that $C$ that has the smallest value. The reason is that you want to explore the clusters in a strict order because the edges may be negative.