Some confusion

When you want to prove that something is $O(n)$, we want to say that it holds in the worst case. When you want to disapprove that something is $O(n)$, you just need to find one example where it doesn’t hold.

Remember your first order logic. If the statement is “there exists a tree such that $h(T) = O(\log n)$, the disapproval of that statement is “there exists no tree such that $h(T) = O(\log n)$. It is NOT “there exists a tree such that $h(T) \neq O(\log n)$. This is quite critical!!

Worst case analysis

This general paradigm is as such: we have an adversary who wants to find the worst possible input for our algorithm. With input sizes of $n$, we denote the worst possible time as $T(n)$. So for example, in a sorting algorithm a typical worst case would be an inverse sort where everything is sorted but backwards.

We will use $T(n)$ in asymptotic analysis, which is detailed below.

Asymptotic analysis

The big idea is that we look at how $T(n)$ behaves for larger and larger $n$, which allows us to disregard everything except for the largest term.

The big pro is that it’s simple and can allow us to compare algorithms, but the con is that it may not represent what we want. For example, 10000000n is “better” than $n^2$

Big O

We seek to answer an important question about our algorithm: how does it perform in the worst possible case?

This is where the big $O()$ notation comes in.

The informal definition

If $T(n)$ is the runtime and $g(n)$ is some simple function, then we say that $T(n) = O(g(n))$ if some constant scaling of $g(n)$ outruns $T(n)$ past a certain point.

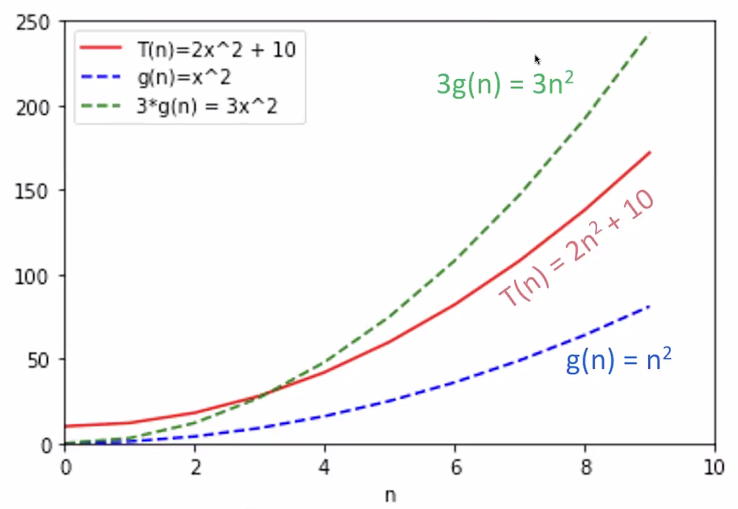
So for example, we say that $T(n)$ in the case above would be $O(n^2)$

Formal definition

Actually, we have much of the framework down already. $T(n) = O(g(n))$ if

“There exists some $c$ such that for all $n$ larger than some constant $n_0$, the runtime is less than $c \cdot g(n)$”

You can chose other values of $c$ and $n_0$. Generally speaking, the larger the $c$, the smaller the $n_0$

Big Omega

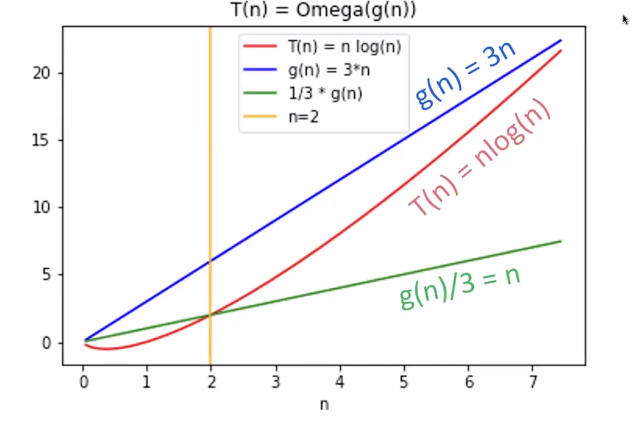
While we started with big O notation as the upper bound, we can also talk about a lower bound $\Omega$ such that $T(n)$ will outrun $\Omega$ past a certain point.

For example, $n \log(n)$ is $\Omega(3n)$, which is shown graphically below

Formalism

It’s very similar. $T(n)$ is $\Omega(g(n))$ if

It should be obvious, but if $f = \Omega(g)$, then $g = O(f)$.

Big Theta

We say that $T(n)$ is $\Theta(g(n))$ if $T(n)$ is $O(g(n))$ and $\Omega(g(n))$.

Now, this doesn’t mean that $T(n) = g(n)$!!! In fact, $n^3 + 3n = \Theta(n^3 - n^2)$. This is because at lower constants $k$, $n^3 + 3n \geq k(n^3 - n^2)$ at sufficiently high $n$, while at larger constants, it’s the other way around. Mathematically, it’s because the intersection is a quadratic, and depending on what the $k$ is, the roots behave differently.

But the general upshot is that only the largest coefficients seem to matter. More on this to come

Solving for $c, n_0$

The easiest way is to set of an inequality, like $n^3 + 3n^2 + 2 \leq cn^3$, and then you do some algebra. For example, you might get $1 + \frac{3}{n} + \frac{2}{n^3} \leq c$. Then, you assign some arbitrary $n = n_0$, and then find a value of $c$ that satisfies this expression. The key insight is that, algebraically, there are infinitely many solutions so you must assign something arbitrarily and solve for the other one

Tightness of asymptotic relationships

We call a bound asymptotically tight if it’s possible to “touch” the bound. For example, $2n^2 = O(n^2)$ is asymptotically tight. We define the little $o$ notation to represent bounds that are not asymptotically tight, like $n = O(n^2)$. More formally:

In other words, no matter how flat or steep we transform this bound function $g$, it is possible to find a point where $f$ does not “touch” the bound again. This is typically a stricter restiction, and as $n → \infty$, $g$ and $f$ become infinitely far apart (which is not guarenteed in asympotitcally tight bounds)

There exists a similar system for $\omega$ notation, where it’s the same as above but just flipped.

Asymptotics in equations and inequalities

Let’s just take a moment to put our hand down on the conventions, because this thing can be confusing. For example, we said something like $n = O(n^2)$. But what does this even mean? Well, this $O(n^2)$ can be thought of as a set, and this equals sign is a membership: $n \in O(n^2)$.

However, in an equation, it’s more of a shorthand anonymous function. For example, $2n^2 + 3n + 1 = 2n^2 + \Theta(n)$, where we collapsed down the $n$ term and all its lessers. We can also understand it as $2n^2 + 3n + 1 = 2n^2 + f(n)$, where $f \in \Theta(n)$.

For equations like $2n^2 + \Theta(n) = \Theta(n^2)$, we say that there is some way of making two functions of order n and n^2 such that this equation is satisfied.

A great diagram

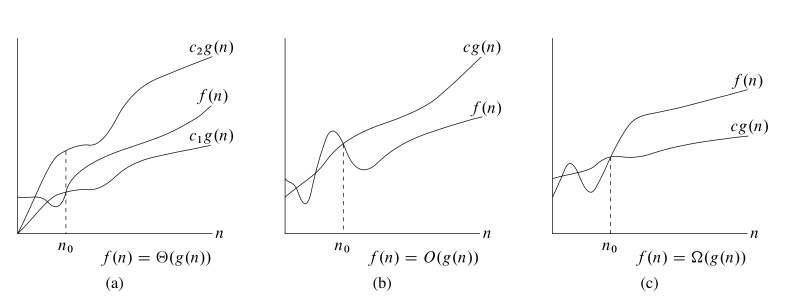
And a good intuition

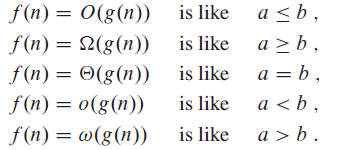
Proof techniques

The simple

To prove that something is of a certain $O$ or $\Omega$, it’s an existence proof. Just find the $c$ and the $n_0$. And this is what a formal proof should look like. Instead of saying something like “the log grows slower than the $n$,” find these two values and it will be true.

To prove that something is not a certain $O()$, we can use a proof by contradiction. Start by assuming that there exists some $c, n_0$ and then show that it’s impossible

Important note

Because this is an existence proof, you need to specify values of $n_0, c$ directly. Then, you can move around the $n$ until you get a bound for $n$, and this should check out with what you defined $n_0$ to be. You shouldn’t start by solving for $n$ and then determining what $c, n_0$ should be. This step can be done first, but then you erase these steps and write a new proof that assumes you have the information at the beginning.

The abstract

Here’s the key that may be confusing. You don’t need to solve for actual values! This is expecially relevant if one of your functions had an anonymous function involved, like $f = 2n^2 + O(n)$.

How would you go about proving that $f = O(n^3)$? Well, we use the facts

1. $cn \leq O(n)$ (definition)

2. $f(n) \leq 2n^2 + cn$ (moving into equation)

3. $f(n) \leq 2n^2 + cn^2 = n^2(2 + c)$

4. And let’s use $c’ = 2 + c$

5. $f(n) \leq c’n^2 \leq c’n^3$, which is what we wanted to show

Do you see how we used this single inequality and propagated it through?

Logical fallacy

When we go to prove complexity, we often require induction. You must pick the constants BEFORE you do the induction. In other words, this is incorrect as the inductive hypothesis: (if we’re proving $O(n)$)

For every $n$, there exists a $c$ such that $T(n) \leq cn$

This is because you can easily define a $c$ for every $n$!! Just make it as large as you want at each time step. The key point is that you should be picking $c$ FIRST. This is what a real inductive hypothesis looks like

There exists a $c$ such that for every $n$, $T(n) \leq cn$.

Subtle difference but very important!

Side note on induction

Induction proofs can go wrong in a few ways. The classical (and most tricky) way that it gets wrong is during the induction step, it uses an inductive hypothesis that we haven’t assumed yet.

The inductive hypothesis can be wrong WRT the problem, but that’s not a problem of the induction itself. For example, we might use our first example (logical fallacy) and prove something by induction. That proof would be flawless, but the end upshot wouldn’t be.